Stochastik

Zu Aufgabe 1

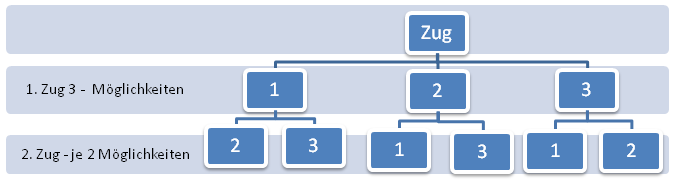
Ganz einfach, man erstellt sich ein Baumdiagramm nennt die Kugeln bspweise 1,2 und 3,

• also ist der Ergebnissraum Ω = $\left [ 123,132,213,231,312,321 \right]$

• (bekomme keine geschweiften Klammern hin) und damit ist die Mächtigkeit |Ω|= $2*3 = 6$

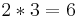
Hier nochmal das Baumdiagramm:

Zu Aufgabe 2

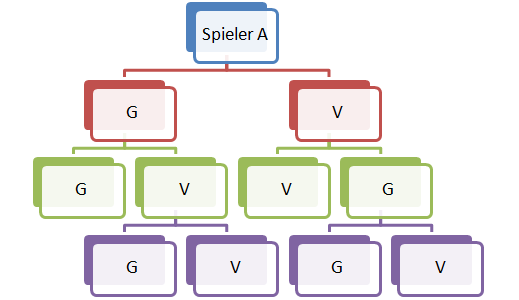
Eigentlich auch ganz einfach, man hat 2 Tennisspieler, die 2 Sätze spielen, Sieger ist derjenige, der als erster 2 Sätze gewonnen hat!

• Also ist der Ergebnissraum wenn man Spieler 1 als A und Spieler 2 als B nennt und einen Satzsieg als G, eine Satzniederlage als V bezeichnet.

Ω = $\left [ AGG,AGVG,AGVV,AVV,AVGV,AVGG,BGG,BGVG,BGVV,BVV,BVGV,BVGG \right]$

• Und damit ist die Mächtigkeit |Ω|= 6*2 = 12

Zu Aufgabe 4

Weiße Kugel= W, Schwarze Kugel=S!

a)

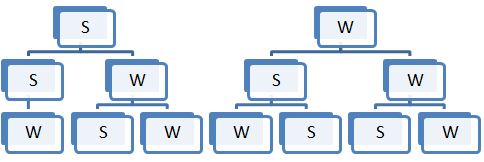
• Eine Urne mit 3 weißen und 2 schwarzen Kugeln, es werden gleichzeitig 3 Kugeln der Urne entnommen. Ein Ergebnissraum wäre z.B

Ω = $\left [ WWW,WWS,WSS \right]$ also wäre die Mächtigkeit |Ω|= 3*1 = 3

b)

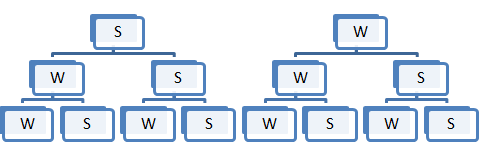
• Nun werden die 3 Kugeln nacheinander ohne zurücklegen herausgenommen!

Ein Ergebnissraum wäre z.BΩ = $\left [WWW,WWS,WSS,WSW,SWS,SSW,SWW\right]$ folglich ist die Mächtigkeit dann |Ω|= 2*2+3

c)

• Teilaufgabe c) ist eigentlich die selbe Aufgabenstellung wie b) nur dass diesmal jede Kugel, die gezogen wurde wieder zurückgelegt wird.

Ein Ergebnissraum wäre z.BΩ = $\left [WWW,WWS,WSW,WSS,SSS,SSW,SWW,SWS\right]$ folglich ist die Mächtigkeit dann |Ω|= 2*2*2=8

Zu Aufgabe 5

Ein Würfel wird solange geworfen bis 6 erscheint aber höchstens 3 mal, sonst würden die Möglichkeiten ins Unendliche gehn, da ja theoretisch die 6 nie auftauchen könnte ! Ausgenommen ist der Fall, dass der Würfel auf der Kante liegen bleibt!

Dann ist ein möglicher Ergebnissraum Ω = $\left [1,2,3,4,5,6,1-1,1-2,1-3...1-6,1-1-1,1-1-2,1-1-3...1-1-6\right]$ Mächtigkeit ist etwas knifflig |Ω|= 5*5*5+(1+5+25)=156

Zu Aufgabe 6

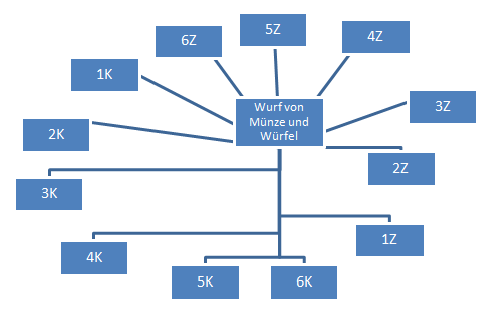
Situation: Eine Münze und ein Würfel werden geworfen und man soll den Ergebnissraum darstellen - dieser ist:

• Ω = $\left [ 1K,2K,3K,4K,5K,6K,1Z,2Z,3Z,4Z,5Z,6Z \right]$

• Mächtigkeit ist somit |Ω|= 6*2=12

• Man geht davon aus, dass der Würfel oder die Münze auf einer geraden Oberfläche geworfen werden und dass beide nicht auf der Kante liegen bleiben! K steht für Kopf, Z steht für Zahl!

wird bis mittwoch abend fertig sein xD