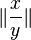Hilfe:Mathematische Formeln ZUMWiki
TeX-Box und Alternativen
TEX-Box
An einer neuen Lösung für die TeX-Box wird derzeit (März 2015) gearbeitet.
TeX equation editor
Mathematische Formeln darstellen
Allgemeine Erklärung
Die Media-Wiki-Software, mit der das ZUM-Wiki betrieben wird, bietet die Möglichkeit an, Formeln anzugeben. Benutzt werden dabei Befehle wie im Schriftsatz-System Latex.
So können auch mit Latex erstellte mathematische Formeln dargestellt werden:
\int \cos\left(x\right)\, \sin\left(x\right) \,\mathrm{d} x = -\frac{\cos\left(2\, x\right)}{4}
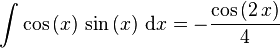
Informationen zu allen möglichen Befehlen und Symbolen finden Sie bei den Latex-Erklärungen aus der Wikipedia12px.
Änderungen ab September 2011
Ersetzungstabelle für neue TEX Version (MimeTEX)
| Funktioniert nicht | Ersatz | Anzeige |
|---|---|---|
| \tfrac | \frac{a} {b} \frac a b |
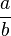 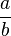
|
| \cong | \tilde = | 
|
| \overrightarrow {ABC} | \vec{AB} | 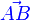
|
| \varnothing {AB} | \empty oder \not {O} | 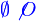
|
| \| | \|| | 
|
| \not\cong | \not {\tilde =} | 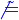
|
| \lbrack \rbrack | \left[ \right] | ![\color{blue}\left[ ... \right]](/images/math/e/2/7/e271495dc86c6b7c3e33d24ae7d61209.png)
|
| \vert | \left| ... \right. | 
|
| \Epsilon | \varepsilon | 
|
| Reelle Zahlen R und entsprechend | \mathbb{R} | 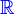
|
Entfallen
| Befehl | Befehl |
|---|---|
| \diamondsuit | \heartsuit |
| \models | \overleftarrow {ABC} |
| \hookleftarrow | \hookrightarrow |
| \longmapsto | \doteq |
| \bowtie | \mho |
| \Box |
Neue Möglichkeiten
| Befehl | Ergibt |
|---|---|
| \color{blue} ABC | 
|
TEST der darstellbaren Zeichen
Die folgenden Absätze stammen von http://www.wikischool.de/wiki/WikiSchool:TeX
| Darzustellen | Syntax | So sieht's gerendert aus |
|---|---|---|
| Standard | abcdefg | 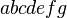
|
| Fett (bold) | \mathbf{abcdefg} | 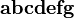
|
| Kursiv (italic) | \mathit{abcdefg}, veraltend: {\it abcdefg} | 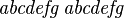
|
| Antiqua (roman) | \mathrm{abcdefg}, veraltend: {\rm abcdefg} | 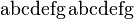
|
| Sans Serif | \mathsf{abcdefg} | 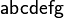
|
| Fraktur (Schrift) | \mathfrak{abcdefg} | 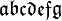
|
| \mathfrak{ABCDEFG} | 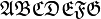
| |
| Kalligraphische Symbole | \mathcal{abcdefghijklm}
\mathcal{nopqrstuvwxyz} |
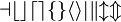
|
| \mathcal{ABCDEFGHIJKLM}
\mathcal{NOPQRSTUVWXYZ} |
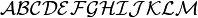
| |
| Zahlenbereiche | \mathbb{N}\mathbb{Z}\mathbb{Q}\mathbb{R}
\mathbb{C}\mathbb{H}\mathbb{F} |
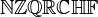
|
| Griechische Buchstaben | \alpha \beta \gamma \delta \epsilon \varepsilon \zeta \eta \theta \vartheta \iota \kappa \lambda \mu \nu
\xi o \pi \varpi \rho \varrho \sigma \varsigma \tau \upsilon \phi \varphi \chi \psi \omega |
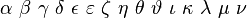
|
| \Gamma \Delta \Theta \Lambda \Xi \Pi \Sigma \Upsilon \Phi \Psi \Omega | 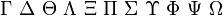
| |
| Imaginärteil, Realteil | \Im\Re (besser: \operatorname{Re},\operatorname{Im}) | 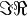 (besser: (besser: 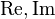 ) )
|
| Funktionsnamen | \sin x (wenn nicht vorhanden: \operatorname{arsinh}) | 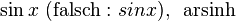
|
| Text, Worte und Wortteile | Schrift, die nicht für Variablen u. ä. steht, immer mit \mathrm{...} setzen, dann stimmt auch die Größe: U_\mathrm{Gesamt} \text{...} funktioniert auch.
\text {ABCabc} ABCabc |
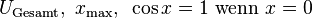
|
Sonderzeichen in TeX
| Darzustellen | Syntax | So sieht's gerendert aus |
|---|---|---|
| Ableitungen | \nabla \partial \mathrm{d} x | 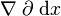
|
| Wurzeln | \sqrt{2}\approx 1{,}4 | 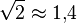
|
| \sqrt[n]{x} | ![\sqrt[n]{x}](/images/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png)
| |
| Winkelgrad | 360^\circ | 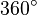
|
| Grad Celsius | 100\,^{\circ}\mathrm{C} | 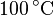
|
| Durchmesserzeichen oder leere Menge | alt: \varnothing neu: \not O | 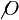
|
| Sonstige Zeichen (Auswahl) | \AA \angle \backslash \bot neu: \Box \clubsuit \diamond \ell \empty \emptyset \infty \exists \flat
\forall \hbar \imath \natural \neg \prime \# \sharp \spadesuit \top \triangle \wp |
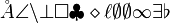
|
Mathematische Symbole
Binäre Operatoren und Vergleiche
|
|
|
Hoch- und Tiefstellungen
| Darzustellen | Syntax | So sieht's gerendert aus |
|---|---|---|
| hochgestellt | a^2 | 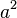
|
| tiefgestellt | a_2 | 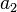
|
| Gruppierung | a^{2+2} | 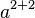
|
| a_{i, j} | 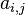
| |
| Kombination hoch & tief | sowohl x_2^3 als auch x^3_2 ergibt | 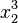
|
| Folge von hoch & tief | {x_2}^3, {x^3}_2 | 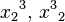
|
| Ableitung (richtig) | x' | 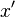
|
| Ableitung (auch richtig) | x^\prime | 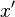
|
| Ableitung (falsch) | x\prime | 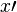
|
| Summe | \sum_{k=1}^N k^2 | 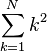
|
| mehrzeilige Summationsgrenzen | \sum_{k\in M,\atop k>5} k | 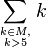
|
| Produkt | \prod_{i=1}^N x_i | 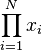
|
| Vereinigung | \bigcup_{\lambda\in\Lambda} A_\lambda | 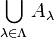
|
| Durchschnitt | \bigcap_{\lambda\in\Lambda} A_\lambda | 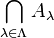
|
| Limes | \lim_{n \to \infty}x_n | 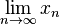
|
| Exponentialfunktion | e^{- \alpha \cdot x^2} | 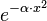
|
| Integral | \int\limits_{-N}^{N} e^x\, \mathrm{d}x | 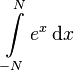
|
| Mehrfachintegral | \iint_a^b \iiint_a^b | 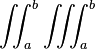
|
| Ringintegral | \oint_c | 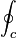
|
| A adjungiert | A^\dagger | 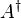
|
Logische Quantoren
Hinweis: Die Verwendung von Quantoren schränkt die Verständlichkeit für Laien und die Lesbarkeit stark ein. Quantoren werden außerhalb der Grundlagen der Mathematik im Regelfall nur als Kurzschreibweise beispielsweise an der Tafel, nicht jedoch in Lehrbüchern oder Fachartikeln verwendet.
| Darzustellen | Syntax | So sieht's gerendert aus |
|---|---|---|
| für alle x | \forall x \, A(x) | 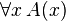
|
| es gibt ein x | \exists x \, A(x) | 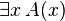
|
| alternativ: | ||
| für alle x | \bigwedge_{x} A(x) | 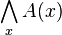
|
| es gibt ein x | \bigvee_{x} A(x) | 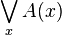
|
Mathematische Akzente
| Darzustellen | Syntax | So sieht's gerendert aus |
|---|---|---|
| Vektorpfeil | \vec a | 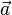
|
| Zeitableitung | \dot a | 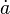
|
| Umlaute | \ddot a | 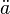
|
| Vektor-Zeitableitung | \dot\vec a | 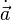
|
| a quer | \bar a | 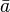
|
| a Tilde | \tilde a | 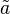
|
| a Dach | \hat a | 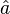
|
| Akzent Grave | \grave a | 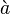
|
| Akzent Acute | \acute a | 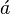
|
| Hatschek | \check a | 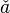
|
| Breve | \breve a | 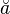
|
| a slash | a\!\!\!/ | 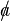
|
Sonstige Markierungen
| Darzustellendes Symbol | Syntax | So sieht's gerendert aus |
|---|---|---|
| Überstreichen | \overline { ... } | 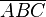
|
| Unterstreichen | \underline { ... } | 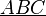
|
| Pfeil drüber | alt:\overrightarrow { ... } neu \vec {ABC} | 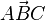
|
| Tilde drüber | \widetilde { ... } | 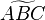
|
| Dach drüber | \widehat { ... } | 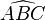
|
| Klammer drüber | \overbrace { ... } | 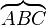
|
| Klammer drunter | \underbrace { ... } | 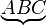
|
Funktionsnamen
|
|
|
Hinweis zu den Funktionsnamen
| Standardfunktionen (richtig) | \ln y +\operatorname{sgn}\, z | 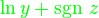
|
| Standardfunktionen (falsch) | ln y + sgn z | 
|
Soll heißen, dass Funktionen immer mit \ begonnen werden sollen. Es werden die Funktionsnamen dann im Gegensatz zu normalem Text nicht kursiv dargestellt. Bei nicht vordefinierten Funktionsnamen wie 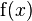 kann mittels \operatorname{f}(x) die für Funktionen übliche Darstellung erreicht werden.
kann mittels \operatorname{f}(x) die für Funktionen übliche Darstellung erreicht werden.
Brüche, Matrizen, mehrzeilige Gleichungen
| Darzustellen | Syntax | So sieht's gerendert aus |
|---|---|---|
| Brüche | \frac{2}{4} oder \frac {13}{27} |  oder oder 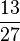
|
| Binomialkoeffizienten | {n \choose k} | 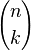
|
| Matrizen | \begin{pmatrix} x & y \\ z & v \end{pmatrix} | 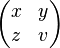
|
| \begin{bmatrix} 0 & \cdots & 1 \\ \vdots & \ddots & \vdots \\ 2 & \cdots & 3\end{bmatrix} | 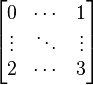
| |
| \begin{Bmatrix} x & y \\ z & v \end{Bmatrix} | 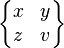
| |
| \begin{vmatrix} x & y \\ z & v \end{vmatrix} | 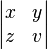
| |
| \begin{Vmatrix} x & y \\ z & v \end{Vmatrix} | 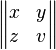
| |
| \begin{matrix} x & y \\ z & v \end{matrix} | 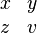
| |
| Fallunterscheidungen | \operatorname{f}(n)=\begin{cases} n/2, & \mbox{wenn }n\mbox{ gerade} \\ 3n+1, & \mbox{wenn }n\mbox{ ungerade} \end{cases} | 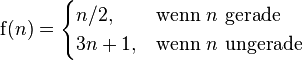
|
| mehrzeilige Gleichungen | \begin{matrix}\operatorname{f}(n+1)&=& (n+1)^2 \\ \ &=& n^2 + 2n + 1\end{matrix} | 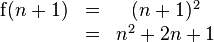
|
Klammern und Begrenzungssymbole
Runde oder eckige Klammern können im Regelfall einfach wie gewohnt eingegeben werden (f(x),a[y]: ![f(x),a[y]\,](/images/math/4/7/5/47520f40abb3eebf4063f5a8dcdd5c23.png) ). Geschweifte Klammern erhält man mit \{ und \}, spitze Klammern mit \langle und \rangle (nicht < und >):
). Geschweifte Klammern erhält man mit \{ und \}, spitze Klammern mit \langle und \rangle (nicht < und >):
richtig: 1=\langle x,y\rangle falsch: 1=<x,y> richtig: 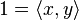
falsch: 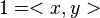
Sollen die Klammern größere Objekte wie z.B. Brüche umschließen, muss man das durch \left und \right ankündigen:
- \left( \frac{x+2}{x^3+7} \right\rangle
-
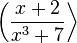
\left und \right müssen paarweise auftreten. Wenn auf einer Seite keine Klammer oder Begrenzungssymbol stehen soll, so folgt einfach ein Punkt \left. oder \right. nach dem left oder right Befehl. (Für den Spezialfall einer Fallunterscheidung gibt es die Umgebung cases, siehe oben.)
Liste der Begrenzungssymbole
| Darzustellen | Syntax | So sieht's gerendert aus |
|---|---|---|
| Runde Klammern | (A) | 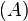
|
| Eckige Klammern | [A]
\left[ \frac xy \right] |
![[A]](/images/math/7/e/2/7e2bf8880d46cb84f91d8740b2659a88.png)
|
| Geschweifte Klammern | \{ A\}
\lbrace \rbrace |
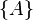
|
| Abrundungsklammer | \lfloor A \rfloor | 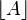
|
| Aufrundungsklammer | \lceil A \rceil | 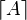
|
| Gewinkelte Klammern | \langle A \rangle | 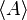
|
| Betragsstriche | \left| A \right|
\| \frac xx \| Achtung: Nur doppelt verwenden! |
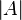
|
| Matrix | \| A \| | 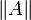
|
| Verwendung von \left. und \right., </ br>wenn man keinen Abgrenzer anzeigen will : | \left. {A \over B} \right\} \to X | 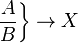
|
große Ausdrücke in Klammern
| Unschön | ( \frac{1}{2} ) | 
|
| Besser | \left( \frac{1}{2} \right) | 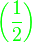
|
Pfeile
|
|
|
Platz zwischen Zeichen
Für manuelle Kontrolle der Leerzeichen stellt Tex folgende Befehle zur Verfügung.
| Darzustellende Leerzeichen | Syntax | So sieht’s gerendert aus |
|---|---|---|
| 8-fach | a \qquad b | 
|
| 4-fach | a \quad b | 
|
| viel Platz | a\ b | 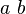
|
| wenig Platz | a\,b | 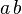
|
| kein Platz | ab | 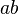
|
| negativer Platz | a\!b | 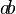
|
Vertikale Ausrichtung
Im Standard-CSS wird der folgende Befehl verwendet:
img.tex { vertical-align: middle; }
Eine Formel wie 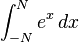 wird damit korrekt ausgerichtet.
wird damit korrekt ausgerichtet.
Wenn das nicht funktioniert kann man stattdessen <font style="vertical-align:-100%;"><math>...</math></font> verwenden und den Wert von vertical-align verändern bis die Ausrichtung stimmt. Jedoch kann die Ausrichtung stark vom verwendeten Webbrowser abhängig sein.
Weitere Beispiele
| Angabe | Syntax | Wie es aussieht |
|---|---|---|
| Schlecht | ( \frac{1}{2} ) | 
|
| Gut | \left ( \frac{1}{2} \right ) | 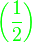
|
| Angabe | Syntax | Wie es aussieht |
|---|---|---|
| runde Klammern | \left ( \frac{a}{b} \right ) | 
|
| eckige Klammern | \left [ \frac{a}{b} \right ] | ![\left [ \frac{a}{b} \right ]](/images/math/8/5/8/8585c96f355f7e301fd5143bea32efaf.png)
|
| geschweifte Klammern | \left \{ \frac{a}{b} \right \} \quad \left \lbrace \frac{a}{b} \right \rbrace | 
|
| spitze Klammern | \left \langle \frac{a}{b} \right \rangle | 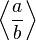
|
| senkrechte Striche und Doppelstriche | \| \frac{a}{b} \| \left \| \frac{c}{d} \right \| |
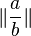 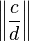
|
| nach unten oder oben offene Klammern: | \left \lfloor \frac{a}{b} \right \rfloor \left \lceil \frac{c}{d} \right \rceil | 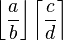
|
| Schrägstriche</td> | \left / \frac{a}{b} \right \backslash | 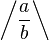
|
| Aufwärts, abwärts Pfeile | \left \uparrow \frac{a}{b} \right \downarrow \quad \left \Uparrow \frac{c}{d} \right \Downarrow \left \updownarrow \frac{e}{f} \right \Updownarrow |
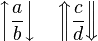 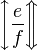
|
| Begrenzer können auch gemischt werden, so lange \left und \right paarweise übereinstimmen. |
\left [ 0,1 \right ) \left \langle \psi \right |
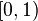 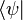
|
| Verwende \left. und \right. wenn keine Klammer erscheinen soll: |
\left . \frac{A}{B} \right \} \to X | 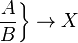
|
| Größe der Begrenzungen | \big( \Big( \bigg( \Bigg( ... \Bigg] \bigg] \Big] \big] |
![\big( \Big( \bigg( \Bigg( ... \Bigg] \bigg] \Big] \big]](/images/math/0/a/2/0a2c41697f07213ddaa59a92738e8bd6.png)
|
| \big\{ \Big\{ \bigg\{ \Bigg\{ ... \Bigg\rangle \bigg\rangle \Big\rangle \big\rangle |

|
Was nur teilweise geht
Binäre Operatoren
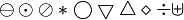
\ominus, \odot, \oslash, \ast, \bigcirc, \bigtriangledown, \bigtriangleup, \diamond, \div, \lhd, \rhd, \unlhd, \uplus, \unrhd
Binäre Vergleiche
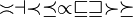
\asymp, \dashv, \Join, \prec, \preceq, \propto, \sqsubseteq, \sqsupseteq, \succ, \succeq
Negation
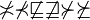
\not\asymp, \not\prec, \not\preqeq, \not\sym, \not\sqsubseteq, \not\sqsupseteq, \not\succ, \not\succeq
Hebräisch
... geht nicht
Pfeile
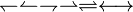
\leadsto \leftharpoondown \leftharpoonup \rightharpoondown \rightharpoonup \rightleftharpoons \longleftrightarrow
Sonstige
| Funktion | kann ersetzt werden durch | Nachteil |
|---|---|---|
| \overset{x}{y} | \begin{matrix} {x} \\ {y} \\ \, \end{matrix} | x wird nicht verkleinert |
| \begin{array}{ll} | \begin{matrix} | wird zentriert ausgerichtet |
| \unit{nF} | {\rm nF}, \mbox{Text}, \mathrm{Text} | Fehlende Semantik |
| \text{Text} | {\rm Text}, \mbox{Text}, \mathrm{Text} | |
| {f\"{u}r} | {f{\ddot u}r} |
Kleine Spielerei:
Fehler beim Parsen(Unbekannte Funktion „\unitlength“): \unitlength{.6} \picture(100) { (50,50){\circle(99)} %%head%% (20,55;50,0;2){\fs{+1}\hat\bullet} %%eyes%% (50,40){\bullet} %%nose%% (50,35){\circle(50,25;34)} %%upper lip%% (50,35){\circle(50,45;34)} %%lower lip%% }
Fehler im Formelsubsystem von Wikipedia
Der ursprüngliche Fehler in der Darstellung wurde durch die Einbindung einer anderen TEX-Anwendung korrigiert.
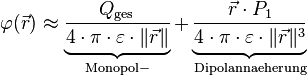
<math>\varphi(\vec r)\approx \underbrace{\frac{Q_{\rm ges}}{4\cdot\pi\cdot\varepsilon\cdot\|
\vec r\|}}_{\rm Monopol-}+\underbrace{\frac{\vec r\cdot P_1}{4\cdot\pi\cdot\varepsilon
\cdot\|\vec r\|^3}}_{\rm Dipolannaeherung}
</math>
Achtung: Umlaute funktionieren nicht, z.B. in Dipolannaeherung.
Anpassungen ab Dezember 2013
Mit dem Umzug auf einen neuen Server mit aktuellerer Software sind einige Anpassungen notwendig geworden, da der neue matt/latex-Parser strikter zu sein scheint als sein Vorgänger.
| alt | neu | Anzeige | siehe auch |
|---|---|---|---|
| <math> E_k_i_n </math> | <math> E_{kin} </math> | 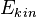
| |
| \blue | \color{blue} | https://en.wikipedia.org/wiki/Help:Displaying_a_formula#Color | |
| \green | \color{green} | ||
| \red | \color{red} | ||
| \box | \Box | ||
| \end{Matrix} | \end{matrix} | ||
| Beispiel | Beispiel | Beispiel | |
| Beispiel | Beispiel | Beispiel | |
| Beispiel | Beispiel | Beispiel | |
| Beispiel | Beispiel | Beispiel | |
| Beispiel | Beispiel | Beispiel | |
| Beispiel | Beispiel | Beispiel | |
| Beispiel | Beispiel | Beispiel | |
| Beispiel | Beispiel | Beispiel | |
| Beispiel | Beispiel | Beispiel | |
| Beispiel | Beispiel | Beispiel | |
| Beispiel | Beispiel | Beispiel | |
| Beispiel | Beispiel | Beispiel | |
| Beispiel | Beispiel | Beispiel | |
| Beispiel | Beispiel | Beispiel |
Linkliste
- Hilfe:TeX12px - eine sehr ausführliche Hilfe zur Benutzung von mathematischen Zeichen mit TeX
- Interaktive Entwicklung der TeX Syntax
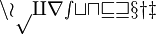
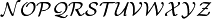
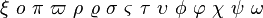
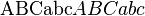
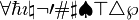
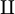
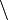
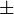
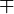
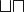
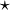

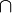


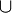

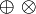
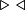
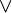
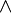
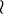
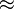
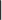
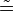

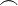

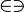
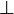
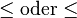
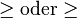
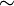
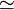
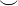

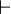
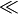
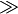
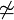
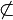
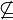
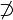

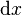
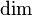
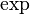
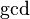
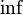
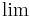
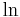
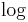
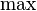
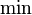
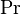
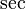
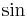
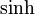
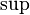
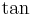
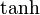
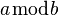
![\left[ \frac xy \right]](/images/math/5/3/2/532a6d97b0493e81f8c7dac247822c00.png)