Abi 2012 Stochastik I Teil B
|
|
|
Für eine Quizshow sucht ein Fernsehsender Abiturientinnen und Abiturienten als Kandidaten. Jeder Bewerber gibt in einem online auszufüllenden Formular die Durchschnittsnote seines Abiturzeugnisses an.
Insgesamt bewerben sich dreimal so viele weibliche wie männliche Personen, wobei 80 % der weiblichen und 75 % der männlichen Bewerber eine Durchschnittsnote von 1,5 oder besser angeben. Bestimmen Sie den Anteil der Personen unter allen Bewerbern, die eine schlechtere Durchschnittsnote als 1,5 angeben.
Aus dem Bewerberfeld werden zwanzig weibliche und zehn männliche Personen zu einem Casting eingeladen, das in zwei Gruppen durchgeführt wird. Fünfzehn der Eingeladenen werden für die erste Gruppe zufällig ausgewählt. Die Wahrscheinlichkeit dafür, dass für die erste Gruppe zehn weibliche und fünf männliche Personen ausgewählt werden, wird mit p bezeichnet. a) Begründen Sie im Sachzusammenhang, dass p nicht durch den Term b) Bestimmen Sie die Wahrscheinlichkeit p mithilfe eines geeigneten Terms. Nach dem Casting stehen die zehn Kandidaten der Quizshow fest.
Im Rahmen der Show müssen Aufgaben aus verschiedenen Fachgebieten gelöst werden. Die Anzahl der von einem Kandidaten zu lösenden Aufgaben aus dem Fachgebiet Mathematik ist gleich der Augensumme, die von ihm bei einmaligem Werfen zweier Würfel erzielt wird. Die beiden Würfel tragen jeweils auf zwei Seitenflächen die Augenzahl 0, auf drei Seitenflächen die Augenzahl 1 und auf einer Seitenfläche die Augenzahl 2. a) Berechnen Sie die Wahrscheinlichkeit dafür, dass der erste Kandidat genau zwei Aufgaben aus dem Fachgebiet Mathematik lösen muss. b) Die Zufallsgröße X beschreibt die Anzahl der von einem Kandidaten zu lösenden Aufgaben aus dem Fachgebiet Mathematik. Der Tabelle kann die Wahrscheinlichkeitsverteilung von X entnommen werden. Ermitteln Sie den fehlenden Wert der Wahrscheinlichkeitsverteilung sowie den Erwartungswert von X.
|

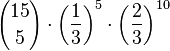 beschrieben wird.
beschrieben wird.



