Abi 2015 Geometrie I Teil A

Mathematik (Bayern): Abiturprüfung 2017 Analysis I - Teil A Download der Originalaufgaben - Lösung zum Ausdrucken

Aufgabe 1 Die Gerade g verläuft durch die Punkte A (0|1|2) und B (2|5|6). a)Zeigen Sie, dass die Punkte A und B den Abstand 6 haben.Die Punkte C und D liegen auf g und haben von A jeweils den Abstand 12. Bestimmen Sie die Koordinaten von C und D. b)Die Punkte A, B und E(1|2|5) sollen mit einem weiteren Punkt die Eckpunkte eines Parallelogramms bilden. Für die Lage des vierten Eckpunkts gibt es mehrere Möglichkeiten. Geben Sie für zwei dieser Möglichkeiten die Koordinatendes vierten Eckpunkts an. [Lösung anzeigen][Lösung ausblenden] 700px

Aufgabe 2 Betrachtet wird die Pyramide ABCDS mit A (0|0|0), B (4|4|2), C (8|0|2), D (4|4|0) und S (1|1|4). Die Grundfläche ABCD ist ein Parallelogramm. a)Weisen Sie nach, dass das Parallelogramm ABCD ein Rechteck ist. b)Die Kante [AS] steht senkrecht auf der Grundfläche ABCD. Der Flächeninhalt der Grundfläche beträgt 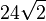$24\sqrt{2}$. Ermitteln Sie das Volumen der Pyramide. [Lösung anzeigen][Lösung ausblenden] 700px