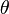Aufbau der Materie und Wärmelehre
Inhaltsverzeichnis[Verbergen] |
Aufbau der Materie und innere Energie
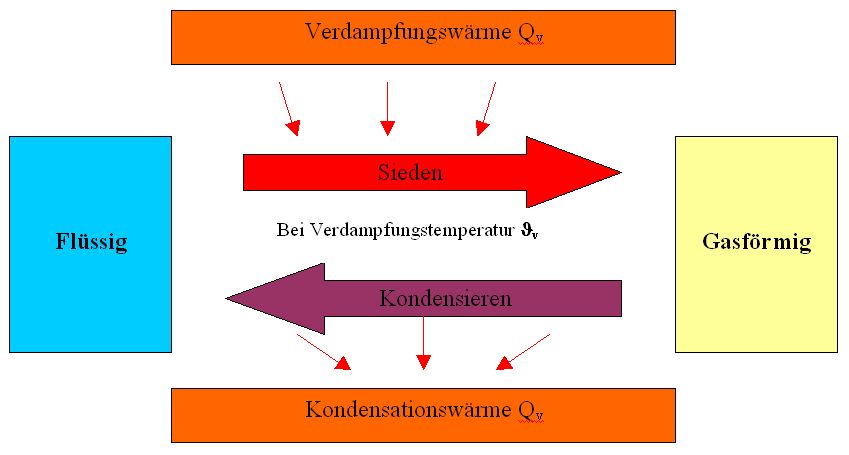
Aggregatszustände> Beschreibung mit Hilfe des Teilchenmodells
Temperatur
|
Änderung der inneren Energie
Energieentwertung
Reversible und irreversible VorgängeEin Vorgang in Natur und/oder Technik kann reversibel oder irreversibel verlaufen. Das bedeutet:
Beispiel: Bewegung der Erde um die Sonne, Fadenpendel (bei kurzer Dauer)
Beispiel: Verbrennen eines Stoffes
|
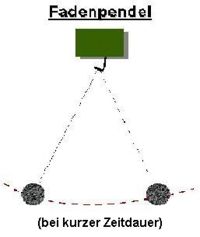
Wirkungsgrad bei irreversiblen VorgängenBei allen irreversiblen Vorgängen wird Energie in Form von Wärme entwertet. Der Wirkungsgrad bei allen Vorgängen, bei denen auch die Innere Energie eine Rolle spielt, ist folglich immer kleiner als 100%, da Innere Energie nie vollständig in andere Energieformen umgewandelt werden kann. Also tritt immer eine Energieentwertung auf. Beispiel: Ein laufender Motor erhitzt sich. Die Wärmeenergie wird durch die Verbrennung des Treibstoffs erzeugt, allerdings kann sie nicht zum Antreiben des Fahrzeugs verwendet werden. Der Energieerhaltungssatz gilt trotzdem.
|
Volumenänderung bei Temperaturänderung
Volumenänderung von Flüssigkeiten(Daniel H.,Patrik H.,Sebastian B.,) Flüssigkeiten (außer Wasser) dehnen sich bei konstanter Temperaturerhöhung linear aus. Volumenausdehnung = Ausgangsvolumen * Volumenausdehnungskoeffizient * Temperaturdifferenz
Einige Beispiele für den Längenausdehnungskoeffizient:
Berechne die Volumenänderung von 76 Liter Benzin, wenn sie sich von 10°C auf 20°C erwärmen. Gegeben: V0=76 l; γ = 0,0010 l/°C; Δδ = 10°C Gesucht: Δ V Lösung: ΔV = V0*γ*Δδ = 76 l * 0,0010 l/°C * 10°C = 0,76 l Das Benzin hat sich um 0,76 l ausgedehnt.
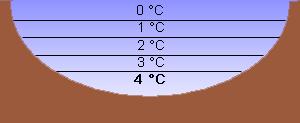
Anomalie des WassersDichte: Wasser hat unter Normaldruck seine größte Dichte bei ca. 4°C und zeigt damit eine Dichteanomalie. Diese besteht darin, dass sich Wasser unterhalb von ca. 4°C bei weiterer Temperaturverringerung, auch beim Wechsel zum festen Aggregatzustand, wieder ausdehnt, was man nur von wenigen Stoffen kennt. Dies führt dazu, dass Eisberge schwimmen. Im flüssigen Zustand herrscht eine Mischung von Ordnung und Chaos, wobei die Moleküle aufgrund ihrer höheren Geschwindigkeit ein größeres Volumen ausfüllen. Es erhöht sich also das Volumen und die Dichte wird damit geringer. Im gasförmigen Zustand ist die maximale Unordnung erreicht und die Atome verteilen sich dementsprechend gleichmäßig über den maximal zur Verfügung stehenden Raum. Festes Wasser hat eine geringere Dichte als flüssiges Wasser, es schwimmt (=anomales Verhalten). Es gilt: -je größer die Temperatur des Wassers, desto kleiner die Dichte -je kleiner die Temperatur des Wassers, desto größer die Dichte Außer:
|
Längenänderung von Festkörpern(von Albin Zehe, Dominik Heusinger, Stefanie Brix) Alle Festkörper dehnen sich bei Erwärmung aus, jedoch nicht alle gleichmäßig (linear). Dafür ist der jeweilige Längenausdehnungskoeffizient verantwortlich. Dieser ist bei jedem Stoff anders. Es kann berechnet werden, um wie viel cm sich ein Stoff ausdehnt und zwar mit dieser Formel: Δl = α ּ lo ּ Δδ oder: Volumenänderung = Volumenausdehnungskoeffizient ּ Ausgangslänge ּ Temperaturänderung
Beispiel: Man erwärmt ein Eisenrohr der Länge 1 Meter um 20°C. Gegeben: α = 0,000.012 1/°C; lo = 1m; Δδ = 20°C Gesucht: Δl Lösung: Δl = α ּ lo ּ Δδ
= 0,000.012 1/°C ּ 1m ּ 20°C
= 0,00024 m
Das Rohr wird dadurch also 0,00024 m länger, das sind 0,24 mm. Einige Beispiele dazu könnt ihr euch hier ansehen, Übungen findet ihr auf dieser und dieser Seite. |
Volumenänderung von GasenAlle Gase dehnen sich unter Wärmezufuhr ungefähr gleich aus, wenn der Druck konstant ist. Die Ausdehnung hängt vom Anfangsvolumen und der Temperaturänderung ab. |