Graph zeichnen
Aus RMG-Wiki
< Mathematik 10 | Die allgemeine Sinusfunktion
Version vom 9. November 2014, 18:49 Uhr von Maria Eirich (Diskussion | Beiträge)
Übungen zu y = a sin b(x - c) + d (Graph zeichnen)
Bewege die Punkte S ("Start"), P ("Periode") und B ("Berg") mit der Maus und zeichne so die Graphen der folgenden Funktionen!
Du kanst Dein Ergebnis kontrollieren, wenn Du Dir den entsprechenden Graph anzeigen lässt.
Wenn Dein Graph nicht mit dem vorgegebenen Graphen übereinstimmt, hilft es Dir, Deine(n) Fehler zu finden, wenn Du Dir die Funktionsgleichung zu dem von Dir eingestellten Graph anzeigen lässt.
Wenn Du Deine(n) Fehler auf diese Weise nicht findest, kannst Du Dir die Koordinaten des Startpunktes S und die Periodenlänge anzeigen lassen.
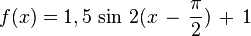
|
Startpunkt
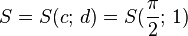 |
Periodenlänge
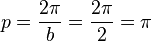 |
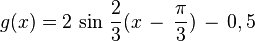
|
Startpunkt
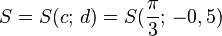 |
Periodenlänge
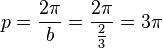 |
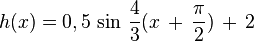
|
Startpunkt
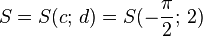 |
Periodenlänge
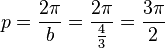 |
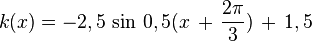
|
Startpunkt
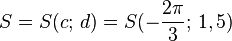 |
Periodenlänge
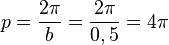 |

