Benutzer:Karina Hetterich

Teste dein Wissen Terme und Zahlen Pluspunkt für eine richtige Antwort:    Minuspunkte für eine falsche Antwort: Ignoriere den Fragen-Koeffizienten: 1. 1.Vereinfache folgende Terme soweit wie möglich. $\frac48 a-( \frac24 a- \frac93 b) =$ $-x(-1-x)-(3+x)(4-x)+12=$ Punkte: 0 / 0 2.Setze im ersten Term die Klammern so, dass eine richtige Termumformung entsteht. $-2a^2+4a \cdot 2 - a = 8a$ Lösung anzeigen Lösung verstecken $(-2a)^2+4a \cdot (2 - a) = 8a$ $-2a^3+2b^3+b^3 = -8a^3+4b^3$ Lösung anzeigen Lösung verstecken $(-2a)^3+2(b^3+b^3) oder -(2a)^3+2(b^3+b^3) = 4a^2+4b^3$ 3.Klammere den größtmöglichen Faktor aus. $12xy^2-18xy+15x^2y$ Lösung anzeigen Lösung verstecken $3xy(4y-6+5x)$ $4(x+y)+5(2x+2y)$ Lösung anzeigen Lösung verstecken $4(x+y)+5\cdot2(x+y) = (x+y)(4+10)=(x+y)\cdot14$ 4.Faktorisiere den Term (mit Hilfe der binomischen Formeln) $9a^2-30a+25$ Lösung anzeigen Lösung verstecken $9a^2-30a+25=(3a-5)^2 2.binomische Formel$ $9a^4-30a^3+25a^2$ Lösung anzeigen Lösung verstecken $9a^4-30a^3+25a^2=a^2(9a^2-30a+25)=a^2(3a-5)^2 a^2 Ausklammern +2.binomische Formel$ $9a^2-25$ Lösung anzeigen Lösung verstecken $9a^2-25=(3a-5)(3a+5) 3.binomische Formel$ 5. Gib die Definitionsmenge an und vereinfache soweit wie möglich $\frac{32a^2+a}{a}$ Lösung anzeigen Lösung verstecken $\mathbb{D} =\mathbb{R} \backslash \{0\} \qquad \frac{32a^2+a}{a}=\frac{a (32a+1)}{a}=32a+1$ $\frac{x^4}{x^6(x-2)}$ Lösung anzeigen Lösung verstecken $\mathbb{D} =\mathbb{R} \backslash \{0,2\} \qquad \frac{x^4}{x^6(x-2)}= \frac{1}{x^2(x-2)}$ 6) Vereinfache soweit wie möglich (a>0) $\sqrt a \cdot (\sqrt a)^3 a^{-3}$ Lösung anzeigen Lösung verstecken $\sqrt a \cdot (\sqrt a)^3 a^{-3} = (\sqrt a)^4 \cdot a^{-3} = a^2 \cdot a^{-3}=a^{2-3}=a^{-1} \frac1 a$ $(16^{\frac1 4} a^{\frac1 a})^4$ Lösung anzeigen Lösung verstecken $(16^{\frac1 4} a^{\frac1 4})^4=((16a)^{\frac1 4})^4=(16a)^{\frac1 4 \cdot 4} =16a$ $8^x:2^x$ Lösung anzeigen Lösung verstecken $8^x:2^x=(8:2)^x=4^x$ Gleichungen 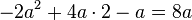Löse die folgenden Gleichungen. Achte auf die Anzahl der Lösungen. Gibt es nur eine Lösungen, trage in das andere Feld "-" ein. Gibt es zwei Lösungen, so ordne diese der Größe nach. $4x+2=14 \qquad \qquad \qquad \qquad x=$                     /                     $-(x+1)=6-(3-x)\qquad \qquad\qquad x=$                     /                     $2x^2-30=68\qquad\qquad \qquad x=$                     /                     $6x^2+66=72x\qquad\qquad \qquad x=$                     /                     $(x-4)(x- \frac 5 2)=0\qquad\qquad \qquad x=$                     /                     $56x+7x^2=0\qquad\qquad \qquad x=$                     /                     $x^5=64\qquad\qquad \qquad x=$                     /                     $x^4-3x^3=0\qquad\qquad \qquad x=$                     /                     $\frac{15}{x-1}=\frac x 2 \qquad\qquad \qquad x=$                     /                     $3^x=27\qquad\qquad \qquad x=$                     /                     $3^x=15\qquad\qquad \qquad x=$                     /                     übrige Lösungen:                     /                     /                     /                     /                     /                     /                     /                     -77-4-2-$\log_{3}{15}$2,56--20$- \sqrt{19}$-6-2,54$\sqrt{19}$12-33-8-30$\log_{15}{3}$112-5 Funktionen 1) Ordne Funktionstyp, Funktionsterm und Funktionsgraph zu $f_1(x)=x^3+1$Gebrochen-rationale FunktionGanzrationale Funktion$f_6(x)=\frac {1}{x^2-4}-2$Exponentialfunktion$f_5(x)=0,5x+1$Trigonometrische Funktion$f_3(x)=-0,2x^4+0,5x^2$Quadratische FunktionGebrochen-rationale Funktion$f_4(x)=0,5x^2+1$$f_2(x)=0,5sinx+1$Lineare FunktionExponentialfunktion$f_7(x)=2\cdot (\frac 1 2)^x$$f_8(x)=2^x-0,5$ 2) Entscheide, ob P(3/-6) auf dem Graphen der Funktion 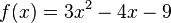$f(x)=3x^2-4x-9$ liegt. (Nein. P liegt unterhalb von Gf) (!Nein. P liegt oberhalb von Gf) (!Ja. P liegt auf Gf)