Homomorphieeigenschaften
Homomorphieeigenschaften des RSA-Verfahrens
Es gilt: 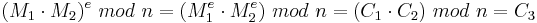 [1]
[1]
Folglich kann Mallory 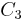 bilden ohne die Nachrichten
bilden ohne die Nachrichten 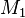 und
und 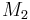 zu kennen, vorausgesetzt er hat die Chiffren
zu kennen, vorausgesetzt er hat die Chiffren 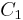 und
und 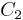 abgefangen.
abgefangen. 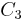 ergibt entschlüsselt eine Nachricht, die die Multiplikation von
ergibt entschlüsselt eine Nachricht, die die Multiplikation von 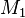 und
und 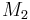 darstellt. In der Regel ergibt dies keinen sinnvollen Klartext, außer es handelt sich bereits bei
darstellt. In der Regel ergibt dies keinen sinnvollen Klartext, außer es handelt sich bereits bei 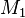 und
und 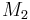 um Zufallszahlen die übertragen wurden, dann wird auch
um Zufallszahlen die übertragen wurden, dann wird auch 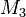 meist wieder eine solche Zahl darstellen. Auf diese Weise hat Mallory die Gelegenheit, den Inhalt der Verschlüsselung zu verändern, ohne dass dies bemerkt wird.[2]
meist wieder eine solche Zahl darstellen. Auf diese Weise hat Mallory die Gelegenheit, den Inhalt der Verschlüsselung zu verändern, ohne dass dies bemerkt wird.[2]
Eine Abwehr hierzu bieten unter anderem die Public-Key Cryptography Standards (PKCS).
PKCS#1-Standard (PKCS = Public-Key Cryptography Standards) ist eine Spezifikation zur Implementierung von RSA-Verfahren. Diese Standards wurden von "RSA Data Security, Inc." festgelegt, als Versuch einen Industriestandard für eine Schnittstelle der Public-Key-Kryptographie zu schaffen.
Insgesamt wurden bisher 12 PKCS-Standards entwickelt.
Wenn es sich bei der RSA-Verschlüsselung beim Klartext um eine Zufallszahl handelt, so sollte durch bestimmte festgelegte Bitmuster zu Beginn der Nachricht sichergestellt werden, dass der Geheimtext auf dem Transportweg z.B. durch Mallory nicht verändert werden kann, um sicherzustellen, dass Bob beim Entschlüsseln erkennen kann, ob die Zufallszahl diejenige ist, die Alice versendet hat. Würde man auf das feste Bitmuster verzichten, so wäre die oben beschriebene Multiplikation der Chiffren möglich. Eine andere Gefahr bestünde darin, dass Bob versehentlich die Nachricht mit dem falschen privaten Schlüssel (z.B. mit dem, den er zum Signieren verwendet) entschlüsselt. Auch in diesem Fall würde sich vermutliche eine Zahl ergeben, die aber falsch wäre.
Der PKCS#1 Version 1-Standard definiert deshalb: Das erste Byte des formatierten Klartextes hat immer den Wert 00000010 als eben beschriebenes Erkennungsmuster, anschließend folgen beliebig viele Zufallsbytes, die ungleich null sind. Nun folgt die Bitfolge 00000000, die den Anfang des tatsächlichen Klartextes markiert.[3]
zurück zum Lernpfad
zurück zur Übersicht

