Kettenbrüche
Kettenbrüche:
„Jede reelle Zahl x element R kann auf genau eine Art durch einen Kettenbruch dargestellt
werden. Der Kettenbruch ist endlich, wenn die Zahl rational ist und unendlich, wenn sie
irrational ist.“[1]
Ich werde hier hautptsächlich auf die Kettenbruchentwicklung der irrationalen Zahlen eingehen, denn die Intervallverhältnisse sind ja (mit Ausnahme von Prime und Oktave) irrationale Zahlen.
Doch was ist ein Kettenbruch?
Im folgenden werde ich die wichtigsten Eigenschaften, vor allem in Hinsicht auf ihre musikalische Anwendung beschreiben. Eine ausführliche Beschreibung findet sich hier.
Man kann jede reelle Zahl x ≥ 0 mit x = 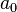 +
+ 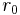 für
für 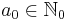 , 0 ≤
, 0 ≤ 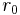 ≤ 1;
≤ 1;
Bsp: In unserem Fall z.B die irrationale (algebraische) Zahl 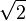
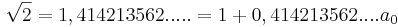 ist das größte Ganze und
ist das größte Ganze und 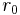 der Rest von x.
der Rest von x.
Für 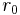 > 0 , gilt:
> 0 , gilt: 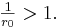
Daraus folgt:
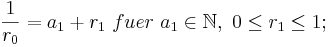
Hierfür erhalten wir:
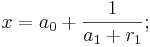 [2]
[2]
Beispiel:
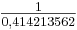 ... = 2 + 0,414213565...
... = 2 + 0,414213565...
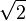 = 1 +
= 1 + 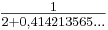
für 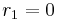 gilt
gilt 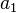 > 0 damit ist der Kettenbruch endlich.
> 0 damit ist der Kettenbruch endlich.
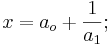
wenn für 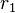 aber gilt:
aber gilt: 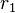 >0 dann ergibt sich:
>0 dann ergibt sich:
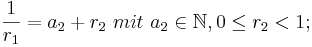
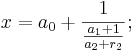
solange gilt 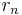 > 0 lässt sich das ganze ins unendliche fortführen.
> 0 lässt sich das ganze ins unendliche fortführen.
Wenn x irrational ist, kann die Kettenbruchentwicklung periodisch sein.
(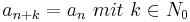 )
)
Dies trifft genau dann zu, wenn x die reelle Lösung einer quadratischen Gleichung 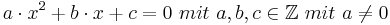
und insbesondere eine algebraische Zahl ist.
Transzendente Zahlen haben keine periodische Kettenbruchentwicklung (Bsp. 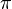 )
)
Die für uns intressante Eigenschaft der Kettenbrüche ist:
Wenn 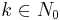 eine gerade Zahl ist, so gilt:
eine gerade Zahl ist, so gilt:
q0 < q2 < … < qk 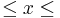 qk+1 < … < q3 < q1;
qk+1 < … < q3 < q1;
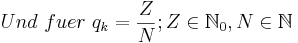
für 0 < n ≤ N gilt für ganze Zahlen z
|x – 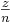 | ≥ |x –
| ≥ |x – 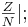
In Worten ausgedrückt: keine rationale Zahl mit einem Nenner > N, approximiert x besser als qk.Referenzfehler: Für ein <ref>-Tag fehlt ein schließendes </ref>-Tag.</ref>
Nun wollen wir die reine und die gleichstufig temperierte Tonskala hier in C-Dur) betrachten:

x gibt dabei die Anzahl der Halbtöne an (vgl Grafik temperierte Stimmung)
y ist die musikalische Tonbezeichnung
H(y) ist das Verhältnis der Tonhöhe zu H(c).
Hier erkennt man, dass die reine Tonskala sich aus der nur mathematisch begründeten gleichstufig temperierten Stimmung durch das Prinzip der Kettenbruch-Approximation ableiten lässt.
weiter zum Vergleich der Stimmungen
zurück zur Übersichtsseite
- ↑ http://www.uni-giessen.de/tomas.sauer/Skripten/Kettenbrueche.pdf [Stand 2010-12-18]
- ↑ vgl. Reimer S.42 f.

