12-Ton-System2
Erweiterung durch neue Töne
Doch welches Verhältnis hat der fehlende Ton (k)?
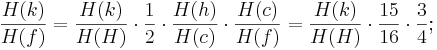
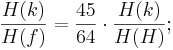
Wenn das Intervall H – k eine reine Quinte ist, so gilt:
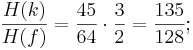
Wenn es eine unreine Quinte ist, ergibt sich:
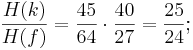 [1]
[1]
Da in der Naturtonreihe der Ton fis dem Verhältnis 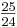 entspricht, ziehen wir dieses Verhältnis für den neuen Ton heran. Also k = fis.
entspricht, ziehen wir dieses Verhältnis für den neuen Ton heran. Also k = fis.
Es wird definiert durch H(fis) = 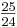
 H(f);
H(f);
Da auf dem fis wiederum keine Quinte intoniert werden kann, muss wiederum ein Ton zugefügt werden.
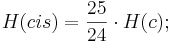
So wird der Tonraum um die folgenden Töne erweitert: fis, cis, gis, dis, ais.
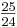
 H(k); für k = f, c, g, d, a.
H(k); für k = f, c, g, d, a.Die Töne werden als Erhöhung bezeichnet. Nun fehlen noch die Quinten abwärts, die Erniedrigungen.
Es werden die Töne: ges, des, as, es, b (=hes) dem Tonraum nach folgendem Schema zugefügt:
H(k-es) = 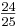
 H(k); für k= g, d, a, e, h.
H(k); für k= g, d, a, e, h.
Allerdings stimmen diese Töne nicht mit den vorher gebildeten Tönen überein.
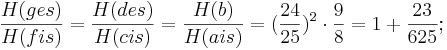
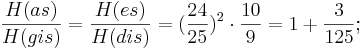
Deshalb haben wir nun 10 neue Töne erhalten, somit hat sich die Anzahl der Töne innerhalb einer Oktave auf 17 erhöht. Das 17 Ton System.
Da auf einem Clavier nun die ganzen Tasten völlig neu eingerichtet werden müssten und der Umfang des Instruments erheblich erhöhen würde, was es fast unmöglich gemacht hätte, auf diesem zu spielen.
Sie waren ungeschlossene Temperaturen, d.h. auch hier entsprachen den 12 Quinten keine 7 Oktaven. Am bekanntesten ist die Groß-Terz Mitteltönigkeit.
Auf die mitteltönigen Temperaturen soll hier nicht weiter gegangen werden. Wer sich trotzdem dafür interessiert der findet hier viele interessante Informationen.
in ihr gilt fis = ges, cis = des, gis = as, dis = es, ais = b;
Dadurch verfälschten sich die jeweiligen Quinten.
Es entstand das 12-Ton-System.
In ihm wurde die Oktave in 12 Tönen eingeteilt, die jeweils einen Halbtonschritt Abstand hatten.
Damit war das System Quinten- und Oktaven-vollständig. Dies steht aber nicht im Widerspruch zu dem vorher Bewiesenen, weil der Begriff der Quinte nun eine offenere Bedeutung hat.
Exkurs: Modulo Rechnung und Quintenzirkel
weiter zur gleichstufig temperierten Stimmung
zurück zur Übersichtsseite
- ↑ vgl. Reimer S.23

