Quint-System3

Die Berechnung der Töne in der pythagoreischen Stimmung:

Allgemein lässt sich hier die Höhe des Tones mit folgender Formel wiedergeben:

$H(t):= \frac{k}{S(t)}$

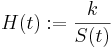
H(t) ist die Tonhöhe; S(t) die Saitenlänge (in einer beliebigen Längeneinheit); k ist eine feste Konstante.

Beim Monochord ist die Länge der schwingenden Saite (oder des Saitenabschnitts) bei konstanter Saitenspannung umgekehrt proportional zur Frequenz.

Für zwei Töne, A und B, gilt, wenn sie eine Oktave auseinanderliegen:

$\frac{H(A)}{H(B)} = \frac{2}{1} ;$

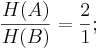
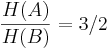$\frac{H(A)}{H(B)} = 3/2$ im Falle einer Quinte;

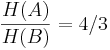$\frac{H(A)}{H(B)} = 4/3$ im Falle einer Quarte;</math>

Dies waren die Proportionen, die besonderen Wohlklang erzeugten. Nun versuchte Pythagoras mit Hilfe der Quinte die Oktave ins 6 gleichgroße Schritte zu zerlegen. Indem er zuerst 2 Quinten aufwärts und dann wieder eine Oktave abwärts ging erhielt er folgendes Verhältnis:

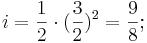$i = \frac{1}{2} \cdot (\frac{3}{2})^2 = \frac{9}{8};$ das Verhältnis der Sekunde.

Mit A0 als Grundton und der HöheH(A0) = 1 konstruierte er die anderen 6 Tonhöhen A1,A2,...A6;

$H(Au) = i^u \cdot H(Ao) = i^u; u= (0),1,2,...,6;$

Der u-te Ton ensteht aus der (2u)-ten Quinte durch Erniedrigung um u Oktaven.

weiter zur Berechnung der Intervalle in der pythagoreischen Stimmung

zurück zur Übersichtsseite

---