Quintenzirkel

Exkurs: Division mit Rest:

„Ist eine Zahl 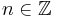$\textstyle n \in \Z$ gegeben und ist $\textstyle m \in \N$, m ≠ 1, eine weiter Zahl, der Divirsor, so kann man n durch m mit Rest dividieren. Das heißt, es gibt eine Zahl k Element Z und einen Rest r, r Element {0, 1, … , m – 1}, so daß

                                              n = k $\cdot$ m + r

gilt.“

Beispiel:

Für n = 25 und m = 7:

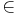25 = 3 $\cdot$ 7 + 4; mit 4 $\textstyle \in$ {0,1,2,3,4,5,6};

Dafür schreibt man: n ≡ r mod (m);

Für alle Töne t der Oktavfolge {…,c,c',...} gilt:

Φ(t) = k $\cdot$ 12 + 0

Für alle Töne der Oktavfolge {…,cis,cis',...}:

Φ(t) = k $\cdot$ 12 +1

„Allgemein wird also der Ton u, das heißt die Oktavfolge {u}, durch den (kleinsten nichtnegativen) Divisionsrest r bei Division durch 12 gekennzeichnet, also durch die für alle Töne der Folge mit einem r Element {0,1,...,11} gemeinsam geltende Kongruenz

Φ(u) ≡ r mod (12).“

u entspricht dem in unserem Beispiel benannten t.

Nun wollen wir die Iterierten Quinten über dem Ton c betrachten.
Es sind die Töne t für die Φ(t) = k $\cdot$ 7 für k = (0),1,2,... gilt.
Dies sind die Töne die die Kongruenz Φ(t) ≡ 0 mod (7) lösen.

Wenn wir nun k Element [0;12] einsetzen erhalten wir folgendes:

 0 $\cdot$ 7 ≡ 0 mod (12) bedeutet {c}

 1 $\cdot$ 7 ≡ 7 mod (12) bedeutet {g}
 2 $\cdot$ 7 ≡ 2 mod (12) bedeutet {d}
 3 $\cdot$ 7 ≡ 9 mod (12) bedeutet {a}
 4 $\cdot$ 7 ≡ 4 mod (12) bedeutet {e}
 5 $\cdot$ 7 ≡ 11 mod (12) bedeutet {h}
 6 $\cdot$ 7 ≡ 6 mod (12) bedeutet {fis}
 7 $\cdot$ 7 ≡ 1 mod (12) bedeutet {cis}
 8 $\cdot$ 7 ≡ 8 mod (12) bedeutet {gis}
 9 $\cdot$ 7 ≡ 3 mod (12) bedeutet {dis}
10 $\cdot$ 7 ≡ 10 mod (12) bedeutet {ais}
11 $\cdot$ 7 ≡ 5 mod (12) bedeutet {f}

12 $\cdot$ 7 ≡ 0 mod (12) bedeutet {c}

Wir sehen, dass jeder Rest mod (12) nur einmal vorkommt und dabei die Werte 0,1,...,11 annimmt, wobei man für k = 12 wieder am Ausgangston angekommen ist.
Die Reihenfolge ergibt den uns bekannten Quintenzirkel



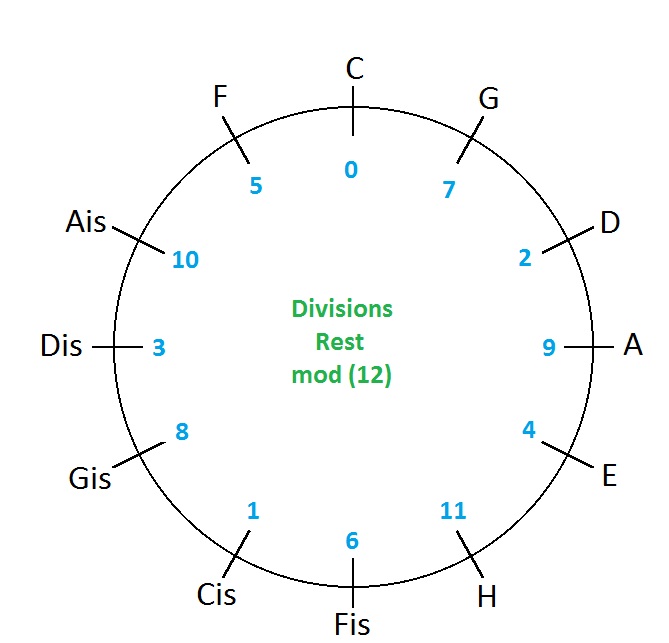
Hinter dem Quintenzirkel steht aus mathematischer Sicht der sogenannte Chinesischen Restsatz (Beweis des Satzes).

weiter zur gleichstufig temperierten Stimmung

zurück zur Übersichtsseite