Aufstellen und Interpretieren von Termen
Aufstellen von Termen
|
|
|
|
|
|
|
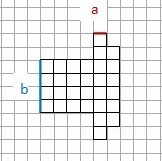
Übertrage die Zeichnung in dein Heft und überlege dir einen Term, mit dem du den Flächeninhalt ausrechnen kannst.
|
|
|
|
Setze nun für a=1cm und b=4cm ein
Erklärung:Um Sachverhalte oder Probleme möglichst kurz zu beschreiben erstellt man einen Term. Dabei solltest du so vorgehen:
Rezept
- Untersuche den Sachverhalt bzw. das Problem und suche nach einer Gesetzmäßigkeit
- Führe eine (oder mehrere) Variable(n) ein
- Stelle den Term auf und überlege dir die zugehörige Definitionsmenge
Beispiel:
Interpretieren von Termen
Erklärung:
|
|
|
|
|
|
|
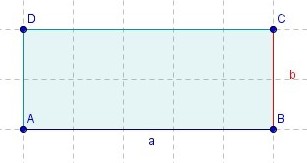
Um einen Term interpretieren zu können, musst du erst die Bedeutung der Variablen klären.
Zum Beispiel beschreibt a•b den Flächeninhalt eines Rechtecks, wenn a und b die Seitenlängen sind.
|
|
|
|
Übungsaufgaben
Aufgabe 1: Übersetze die Rechenvorschrift in einen Term:
a) Addiere 2 zum Quadrat von x
b) Addiere 6 zum vierfachen der Zahl n
c) Multipliziere die Summe aus b und der Zahl 7 mit 4
d) Multipliziere x mit seiner Gegenzahl
e) Multipliziere den Vorgänger der natürlichen Zahl n mit seinem Nachfolger
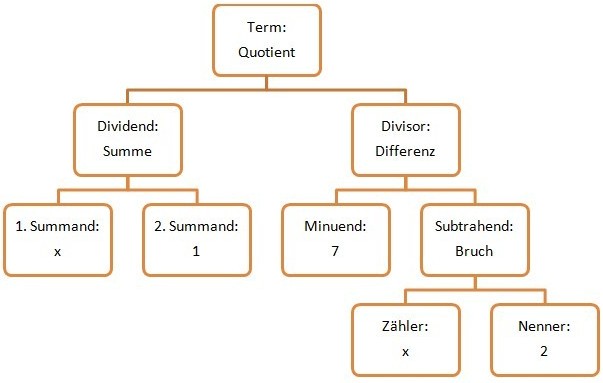
Aufgabe 2:Gib den Term zu folgendem Gliederungsbaum an und berechne seinen Wert für x=4!
Aufgabe 3:
|
|
|
|
|
|
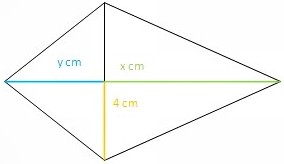
Gib einen Term an, der den Flächeninhalt der abgebildeten Figur berechnet.
Berechne anschließend den Flächeninhalt der Figur, indem du für die Variablen die angegebenen Zahlen einsetzt.
- A(8cm;2cm)
- A(10cm;5cm)
- A(12cm;9cm)
- A(15cm;13cm)
Hinweis: Die Figur ist Achsensymmetrisch
|
|
|
|
Aufgabe 4:Laura hat zu schnell von der Tafel abgeschrieben. Dabei hat sie die Werte der Variablen vergessen, nur die Ergebnisse hat sie noch. Hilf ihr die passenden Werte für die Variablen zu finden, wenn der Term T(n)=n
2+2 lautete.
Warum gibt es meist zwei Möglichkeiten?
a) T(?)= 18
b) T(?)= 38
c) T(?)= 3
d) T(?)= 6



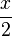 )
)
 ) = 5:(7-2) = 5:5 = 1
) = 5:(7-2) = 5:5 = 1


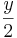 cm)+(8cm•
cm)+(8cm•
