- Aufgabe 1
- a) Gegeben sind die in
 definierten Funktionen definierten Funktionen
g: x → 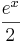 , g*:x → , g*:x → 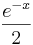 und f1: x → und f1: x → 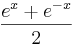 . .
- Zeichnen Sie mit Hilfe der Funktionswerte g(-1) , g(1) und g(2) den Graphen von g im Bereich -2
 x x 2 in ein Koordinatensystem mit der Längeneinheit 2 cm. 2 in ein Koordinatensystem mit der Längeneinheit 2 cm.
- Erläutern Sie, wie der Graph von g* aus dem Graphen von g und schließlich der Graph von f1 aus den Graphen von g und g* entsteht. Zeichnen Sie die Graphen von g* und f1 in das vorhandene Koordinatensystem.
6 BE
Hinweis: Die Entstehung von Graphen aus anderen Graphen kann in diesem Lernpfad wiederholt werden.
- [Lösung anzeigen][Lösung ausblenden]
- Die Funktion f1 gehört der Funktionenschar fk: x →
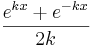 mit D = mit D =  und k und k  + an. + an.
- Der Graph von fk wird mit Gk bezeichnet.
- b) Welches Symmetrieverhalten weist Gk auf?
- Bestimmen Sie das Monotonieverhalten von fk und geben Sie die Koordinaten des Extrempunktes an.
5 BE
- [Lösung anzeigen][Lösung ausblenden]
- c) Nun wird die Integralfunktion Fk
- x →
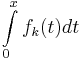 mit dem Definitionsbereich mit dem Definitionsbereich  betrachtet. betrachtet.
- Bestimmen Sie ohne Berechnung der integralfreien Darstellung von Fk das Symmetrie-, Monotonie- und Krümmungsverhalten des Graphen von Fk (kurze Begründung).
6 BE
- [Lösung anzeigen][Lösung ausblenden]
- d) Ermitteln Sie eine integralfreie Darstellung von F1(x) und zeigen Sie die Gültigkeit der Beziehung [f1(x)]2=1+[F1(x)]2 für alle x
  . .
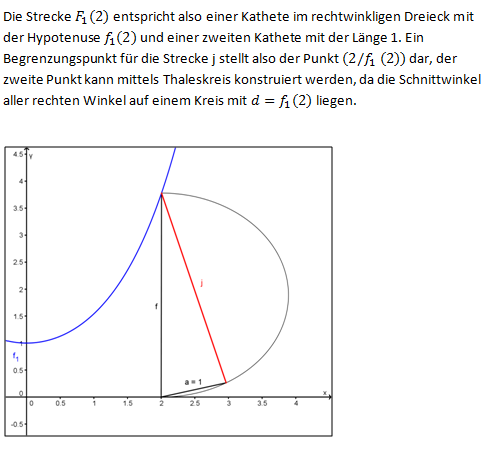
- Konstruieren Sie mittels dieser Beziehung den Wert J des Integrals
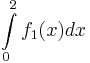 als Streckenlänge in Ihrer Zeichnung und markieren Sie die zugehörige Strecke farbig. als Streckenlänge in Ihrer Zeichnung und markieren Sie die zugehörige Strecke farbig. 8 BE
- [Lösung anzeigen][Lösung ausblenden]
|
 definierten Funktionen
definierten Funktionen 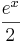 , g*:x →
, g*:x → 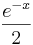 und f1: x →
und f1: x → 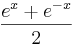 .
.
 x
x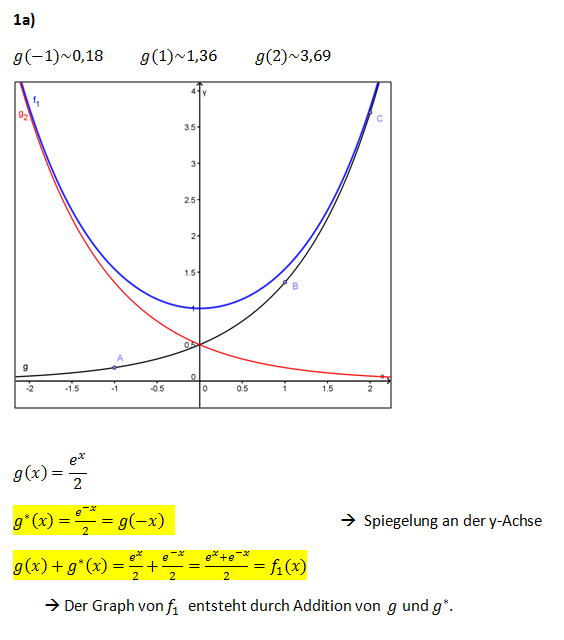
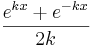 mit D =
mit D = 

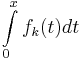 mit dem Definitionsbereich
mit dem Definitionsbereich 
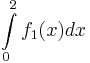 als Streckenlänge in Ihrer Zeichnung und markieren Sie die zugehörige Strecke farbig.
als Streckenlänge in Ihrer Zeichnung und markieren Sie die zugehörige Strecke farbig. 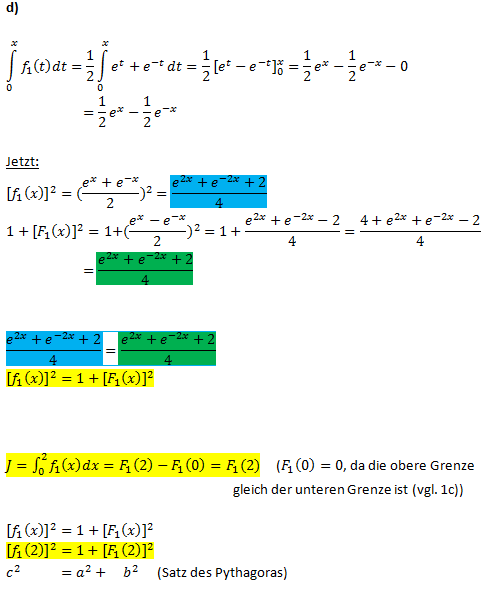
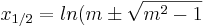 ]
]



