- Aufgabe 1
In einem kartesischen Koordinatensystem des IR3 sind die Punkte M(−2 | 4 |1), S(6 | 8 | 9), P(4 | −8 |1) sowie die Gerade g : 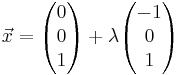 , λ ∈ IR gegeben.
Die Strecke [MS] ist die Höhe eines geraden Kreiskegels. Sein Grundkreis k um den Punkt M hat den Radius , λ ∈ IR gegeben.
Die Strecke [MS] ist die Höhe eines geraden Kreiskegels. Sein Grundkreis k um den Punkt M hat den Radius 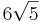 und liegt in der Ebene E. und liegt in der Ebene E.
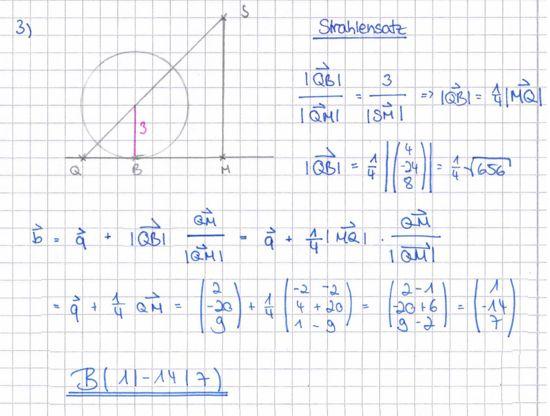
a) Ermitteln Sie eine Gleichung der Ebene E in Normalenform und zeigen Sie, dass der Punkt P auf dem Grundkreis k liegt.
[Zur Kontrolle: E : 2x1 + x2 + 2x3 − 2 = 0] 5 BE
- [Lösung anzeigen][Lösung ausblenden]
1.Lösung Ebene erstellen
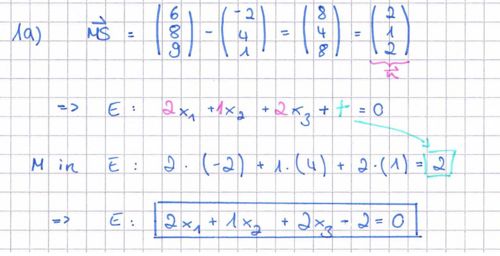
- Bemerkung
Zu beweisen ist, dass P AUF nicht innerhalb von k liegt. Deswegen muss als Bedingung MP = r und nicht MP <= r gelten
2.Lösung Ebene erstellen

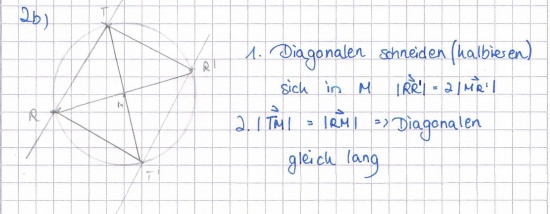
b) Zeigen Sie, dass die Gerade g in der Ebene E liegt, und bestimmen Sie die Koordinaten der Schnittpunkte R und T von g und k. (Der Punkt mit positiver x1-Koordinate wird mit R bezeichnet.)
[Teilergebnis: R(8 | 0 | −7), T(−10 | 0 |11)] 7 BE
- [Lösung anzeigen][Lösung ausblenden]

Bestimmung der Schnittpunkte
1. Lösung: g in k

2. Lösung: allgemeiner Geradenpunkt

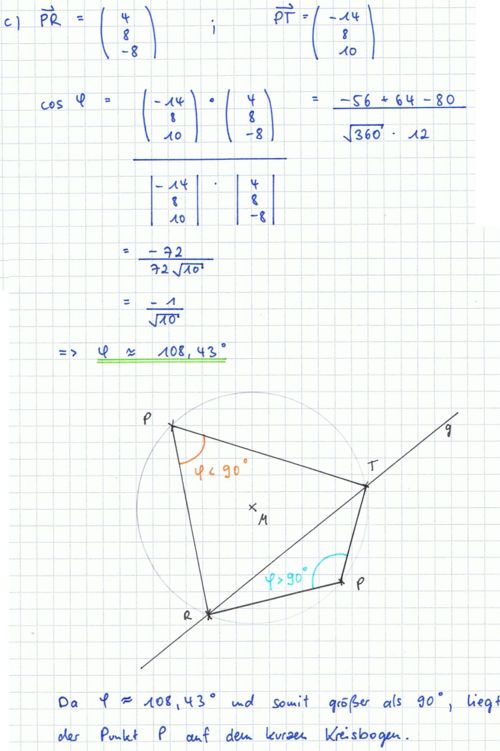
c) Die Gerade g teilt den Grundkreis k in einen kurzen und einen langen Kreisbogen. Berechnen Sie den Winkel ϕ, den die Vektoren 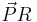 und und 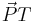 einschließen, und geben Sie an, auf welchem der beiden Bögen der Punkt P liegt. Begründen Sie Ihre Antwort. einschließen, und geben Sie an, auf welchem der beiden Bögen der Punkt P liegt. Begründen Sie Ihre Antwort. 6 BE
- [Lösung anzeigen][Lösung ausblenden]
|
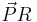 und
und 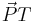 einschließen, und geben Sie an, auf welchem der beiden Bögen der Punkt P liegt. Begründen Sie Ihre Antwort.
einschließen, und geben Sie an, auf welchem der beiden Bögen der Punkt P liegt. Begründen Sie Ihre Antwort. 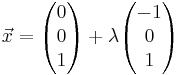 , λ ∈ IR gegeben.
Die Strecke [MS] ist die Höhe eines geraden Kreiskegels. Sein Grundkreis k um den Punkt M hat den Radius
, λ ∈ IR gegeben.
Die Strecke [MS] ist die Höhe eines geraden Kreiskegels. Sein Grundkreis k um den Punkt M hat den Radius 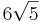 und liegt in der Ebene E.
und liegt in der Ebene E.