2005 I

Leistungskurs Mathematik (Bayern): Abiturprüfung 2005 Infinitesimalrechnung 1 Lösung von Daniel Greb, Sebastian Waldhäuser Angabe gesamte Lösung

Aufgabe 1 Gegeben ist die Schar der in |R definierten Funktionen fk(x)=(x2 + 1 - k)e-x mit k E |R Der Graph von fk wird mit Gkbezeichnet. a) Untersuchen Sie fk auf Nullstellen in Abhängigkeit von k. Bestimmen Sie das Verhalten von fk für x->-8 und x->+8. Lösung anzeigen Lösung verstecken 750px 4 BE b) Zeigen Sie, dass sich je zwei verschiedene Graphen Gk nicht schneiden, einander aber beliebig nahe kommen. Lösung anzeigen Lösung verstecken 750px 4 BE c) Für welche Werte von k besitzt Gk mindestens eine waagrechte Tangente? Zeigen Sie, dass sie Punkte von Gk mit waagrechter Tangente auf dem Graphen W der Funktion w: x->2xe-x mit x E |R liegen. Lösung anzeigen Lösung verstecken 750px 7 BE d) Die unten stehende Abbildung zeigt die Graphen G1 und W. Zeichnen Sie unter Verwendung aller bisherigen Ergebnisse den GRaphen G2 in die Abbildung ein. 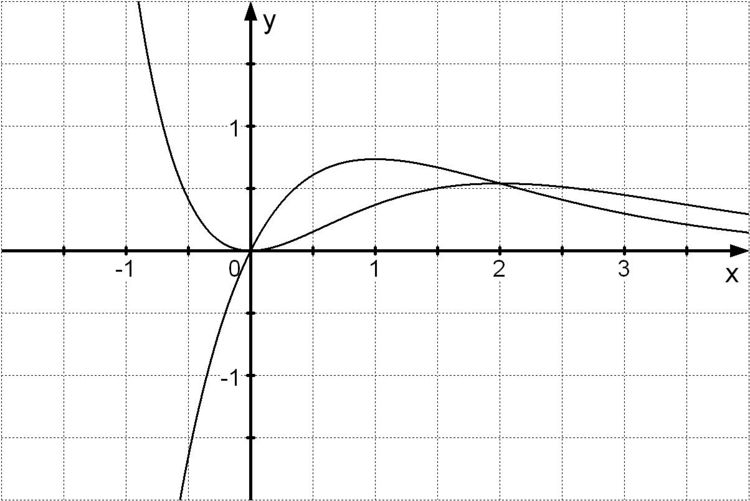Lösung anzeigen Lösung verstecken 750px 5 BE e) Bestätigen Sie, dass für k E |R gilt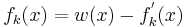: $f_k(x) = w(x) -f_{k}^{'}(x)$ Der Grapg G1 begrenzt im ersten Quadranten mit der x-Achse ein sich ins Unendliche erstreckendes Flächenstück mit endlichen Inhalt. Berechnen Sie diesen Flächeninhalt der obigen Beziehung. Lösung anzeigen Lösung verstecken 750px <dic align="Right">7 BE