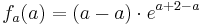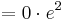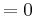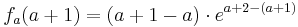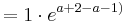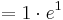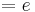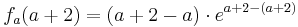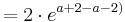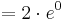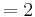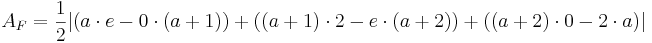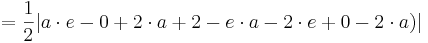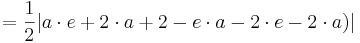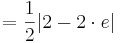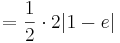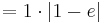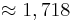Lösung von Teilaufgabe d

Kongruenz der Dreiecke

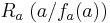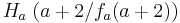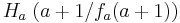Die Dreiecke werden durch die Punkte $\; R_a\;( a / f_a (a))$, $H_a\; ( a + 2 / f_a ( a + 2 ))$ und $H_a\; ( a + 1 / f_a ( a + 1 ))$ festgelegt.

1.Punkt : 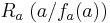$\; R_a\;( a / f_a (a))$

$f_a (a) = ( a - a )\cdot e^{ a + 2 - a }$

$= 0\cdot e^{ 2 }$

$= 0\;$

Der Punkt R_a liegt für alle a bei R_a ( a / 0 )

2.Punkt : 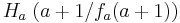$H_a\; ( a + 1 / f_a ( a + 1 ))$

$f_a (a+1) = ( a + 1 - a )\cdot e^{ a + 2 - (a+1) }$

$= 1 \cdot e^{ a + 2 - a-1) }$

$= 1 \cdot e^{1}$

$= e\;$

Der Punkt H_a liegt für alle a bei H_a ( a + 1 / e )

3.Punkt : 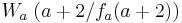$W_a\;( a + 2 / f_a ( a + 2 ))$

$f_a (a+2) = ( a + 2 - a )\cdot e^{ a + 2 - (a+2) }$

$= 2 \cdot e^{ a + 2 - a-2) }$

$= 2 \cdot e^{0}$

$= 2 \;$

Der Punkt W_a liegt für alle a bei W_a ( a + 2 / 2 )

Mit den drei bestimmten Punkten R_a, H_a und W_a lässt sich erkennen, dass die Dreiecke für alle verschiedene a kongruent sind. Die y-Werte aller drei Punkte sind für alle a identisch. Daraus schließt man, dass sich die drei Punkte nur auf der x-Achse beziehungsweise auf einer Parallelen zur x-Achse, immer um den gleichen Wert, nämlich um a, verschieben. Da sich die Punkte nur auf Parallelen zur x-Achse verschieben, heißt das natürlich auch, dass sich das Dreieck nur auf der x-Achse verschiebt und somit immer kongruent ist.

Flächeninhalt des Dreiecks

$im R^{2}: A = \frac{1}{2} | ( a_1\cdot b_2 - a_2\cdot b_1) + ( b_1\cdot c_2 - b_2\cdot c_1 ) + ( c_1\cdot a_2 - c_1\cdot a_2 ) |$

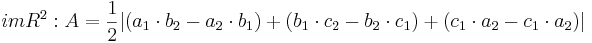
siehe Formelsammlung Seit 81

$Definiere: \;$
$A\; (\;a_1 \;/\; a_2 \;) = R_a \;(\; a \;/\; 0\; )$
$B\; (\;b_1 \;/\; b_2 \;) = H_a \;( \;a + 1\; /\; e \;)$
$C\; (\;c_1 \;/\; c_2 \;) = W_a \;(\; a + 2 \;/ \;2 \;)$

$A_F = \frac{1}{2} | ( a\cdot e - 0\cdot (a+1)) + ( (a+1)\cdot 2 - e\cdot (a+2) ) + ( (a+2)\cdot 0 - 2\cdot a ) |$

$= \frac{1}{2} | a\cdot e - 0 + 2\cdot a + 2- e\cdot a -2\cdot e + 0 - 2\cdot a ) |$

$= \frac{1}{2} | a\cdot e + 2\cdot a + 2- e\cdot a -2\cdot e - 2\cdot a ) |$

$= \frac{1}{2} | 2 -2\cdot e |$

$= \frac{1}{2}\cdot2 | 1 - e |$

$= 1\cdot | 1 - e |$

$= | 1 - e |\;$

$\approx 1,718$

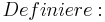
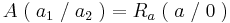
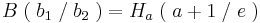
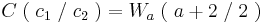
Der Flächeninhalt beträgt, unabhängig von a, | 1 - e |

Grafik zur Kongruenz und zum Flächeninhalt der Dreiecke

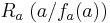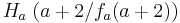
1. In der Graphik lässt sich deutlich erkennen, das die Dreiecke, bestehend aus den Punkten $\; R_a\;( a / f_a (a))$, $H_a\; ( a + 2 / f_a ( a + 2 ))$
und 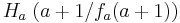$H_a\; ( a + 1 / f_a ( a + 1 ))$ für alle a kongruent (dekungsgleich) sind.
2. Aus erstens folgt zwangsweise auch, dass der Flächeninhalt für alle a gleich groß bleibt. Dies lässt sich auch deutlich in der Graphik erkennen.