Geometrie

zurück: Jahr der Mathematik

Geometrische Bilder

Kreisbilder mit GeoGebra

mehr Kreisbilder

Schrägbilder

von Dominique Gründler

Isometrische Schrägbilder von Gebäuden

Isometrie ist eigentlich fast das gleiche wie Geometrie, aber eben doch ein bisschen anders, da dreidimensional dargestellt. Am Anfang habe ich nur ein paar Quadrate und Rechtecke gezeichnet, aber dann kam ich auf die Idee, verschiedene Formen in 3D zu zeichnen, wie ihr auf dem Bild rechts sehen könnt.

Wenn ihr wissen wollt wie Schrägbilder funktionieren, dann lest euch den unteren Text durch.

Erklärung zu Schrägbildern

Um sich einen Körper besser vorstellen zu können, zeichnet man von ihm ein Schrägbild. Kanten, die in Wirklichkeit parallel sind, sind auch im Schrägbild parallel. Kanten, die in Wirklichkeit aufeinander senkrecht stehen, müssen im Schrägbild nicht aufeinander senkrecht stehen.

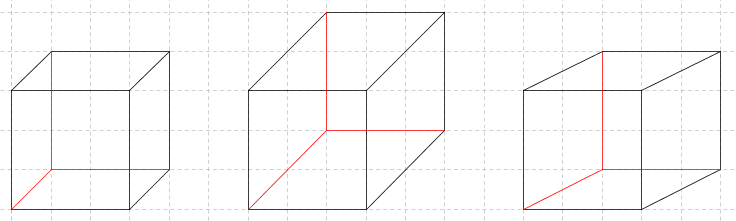
Die Zeichnungen zeigen verschiedene Schrägbilder eines Würfels.

Welches der drei Zeichnungen sieht am ehesten nach einem Würfel aus?

Übung für Anfänger: Schrägbild eines Würfels

Nehmt erstmal ein kariertes Blatt Papier und einen Bleistift zur Hand. Vielleicht noch ein Geodreieck, falls ihr es braucht.

Zeichnet jetzt ein Quadrat.

Zeichnet dann, in einem Winkel von 45°, drei Schrägen an die rechten drei Ecken. Wenn ihr das gemacht habt, verbindet sie miteinander.

So, nun seid ihr fast fertig. Aber ihr müsst, um das Schrägbild noch offensichtlicher zu machen, eine gestrichelte Schräge an der unteren linken Ecke nach innen zeichnen. Zeichnet danach eine gestrichelte, senkrechte Linie nach oben, vom Ende der gestrichelten Schräge.

Gut!

Nun kommt eine gestrichelte, waagrechte Linie nach rechts, wieder vom Ende der gestrichelten Schräge.

Geschafft!!!!!

Nun habt ihr das Schrägbild eines Würfels.