Benutzer:Gebauer David
Aus RMG-Wiki
Version vom 2. April 2009, 09:56 Uhr von Gebauer David (Diskussion | Beiträge)
((Benutzer:Gebauer David/Revolution 1848)) Hausaufgabe vom 23.09.2008
Infinitesimalrechnung
1. Gegeben ist die Schar der in  definierten Funktionen
definierten Funktionen 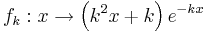 mit
mit 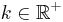 . Der Graph von
. Der Graph von 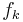 wird mit
wird mit 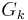 bezeichnet.
bezeichnet.
a) Bestimmen Sie die Schnittpunkte von 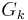 mit den Koordinatenachsen und untersuchen Sie das Verhalten von
mit den Koordinatenachsen und untersuchen Sie das Verhalten von 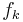 für
für 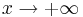 und
und 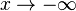 .
.
b) Bestimmen Sie Lage und Art des Extrempunktes von 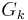 .
.  zur Kontrolle:
zur Kontrolle: 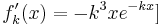
Lösung:
![f'_k(x)=k^2e^{-kx}(-k)=-k^2[(kx+1)e^{-kx}-e^{-kx}]=-k^3xe^{-kx}](/images/math/b/2/e/b2e2bc5fca03cbdebde56f76575b0dd7.png)
Lösung: c