Die Betrachtung des Intervallbegriffs aus musikalischer Sicht
Die Betrachtung des Intervallbegriffs aus musikalischer Sicht:
Die Übertragung des Begriffes Intervall auf den Abstand zweier Töne gab es bereits in der Antike (Harmoniam autem ex intervallis sonorum nosse possumus, Cicero, Tusc. I 41). Im Mittelalter wurde häufiger die Definiton von Boethius verwendet. (Intervallum est vocis a voce, seu soni acuti gravisque distantia, De institutione musica V). [1]In der heutigen Zeit wird zur Messung der Größe der Intervalle die Cent-Rechnung benutzt.
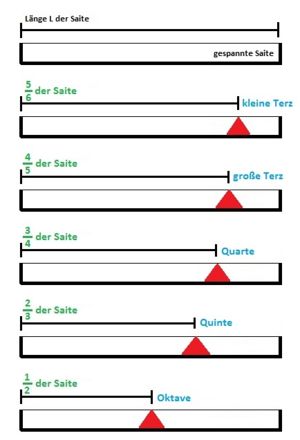
Die verschiedenen Intervalle wurden in der Antike von den Pythagoreern experimentell vom Monochord abgeleitet. Die abgeleiteteten Zahlenverhältnisse wurden durch die Proportionen der klingenden Seitenlängen hörbar gemacht. Pythagoras von Samos erkannte, der Schmiedlegende nach, als erster den Zusammenhang zwischen den Zahlenverhältnissen und den Tonabständen.
Er fand heraus, dass die Tonhöhe einer schwingenden Seite abhängig von der Länge ist. Wird die Länge halbiert, bekommt man einen Ton, der sich eine Oktave über dem Grundton befindet. Wird die Saite gedrittelt so ergibt sich eine Quinte. Analog dazu ergeben sich Quarte, große und kleine Terz, durch ein viertel, fünftel und sechstel der Saitenlänge.[2]
Descartes leitete in seinem Werk "musicae compendium" (1650) die Proportionen folgendermaßen ab:
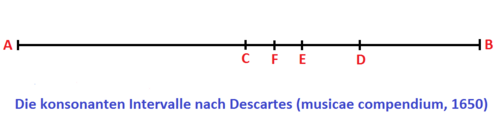
Dies soll die Saite eine Monochords darstellen. Der Anfang der Saite befindet sich bei A, das Ende bei B. Nun wird die Saite in der Mitte, durch einführen eines Steges bei C geteilt. Daraus ergibt sich AC:AB = 1:2. Man erhält die Oktave. Um die Quinte zu erhalten wird die Strecke CB halbiert. Die Hälfte der Strecke CB entspricht D. Nun gilt: AC:AB = 2:3. Da sich Quinte und Quarte zur Oktave ergänzen folgt für die Quarte: AD:AB = 3:4. Um die große Terz zu erhalten wird CD im Mittelpunkt E geteilt. AC:AE = 4:5. Für die kleine Terz gilt: AE:AD = 5:6. Nun teilt man CE im Mittelpunkt F um den großen Ganzton zu erhalten: AC:AF = 8:9 und der kleine Ganzton: AF:AE = 9:10 [3]
Die Tonraumzahlen
zurück zur Übersichtsseite