Erweiterung des Tonsystems
Beweis, das es kein Tonsystem gibt, das sowohl Oktaven- als auch Quintenvollständig ist:
Wir nehmen nun ein Tonsystem her, dass Oktaven-vollständig ist. Die Oktave wird durch die beiden Töne a und a' begrenzt. Zwischen diesen beiden Tönen liegt nun eine endliche Anzahl anderer Töne.
Nun nehmen wir zusätzlich noch an das das System Quinten-vollständig ist. Nun bilden wir ausgehend von u0:= a die Töne u1, u2, …., uj, im Quinten-Abstand.
Die Tonhöhe des j-ten Tons ist:
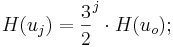
Nun reduzieren wir den Ton um m Oktaven und erhalten einen Ton der in dem gewünschten Intervall a a' liegt:
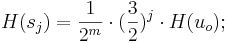
Wenn wir die Rechnung nun für j = 1 , j = 2, …, durchführen erhalten wir die Töne s1,s2,…,die im Intervall [a;a'[ liegen. Wegen dem endlichen Tonvorrat müssen 2 Töne identisch sein: sj und sk, für k ≠ j;
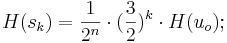
Weil wir definiert haben das 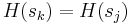 ist, gilt:
ist, gilt:
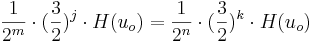
Nun formen wir die Gleichung um:
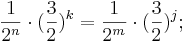
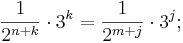
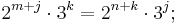
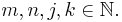
Wie deutlich wurde gibt es sowohl bei pythagoreischer Stimmung als auch bei der natürlichen Stimmung ein Problem mit den reinen Quinten.
Es fiel auf das man eine Oktave (a, a') in keiner Weise, durch wie viele Töne auch immer teilen kann, dass das System das dabei entsteht sowohl Quinten – als auch Oktaven-vollständig ist.
Dies wollen wir nun mathematisch Beweisen.
Wir nehmen nun ein Tonsystem her, dass Oktaven-vollständig ist. Die Oktave wird durch die beiden Töne a und a' begrenzt. Zwischen diesen beiden Tönen liegt nun eine endliche Anzahl anderer Töne.
Nun nehmen wir zusätzlich noch an das das System Quinten-vollständig ist. Nun bilden wir ausgehend von uo:= a die Töne u1, u2, …., uj, im Quinten-Abstand.
Die Tonhöhe des j-ten Tons ist:
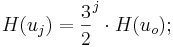
Nun reduzieren wir den Ton um m Oktaven und erhalten einen Ton der in dem gewünschten Intervall a a' liegt:
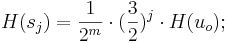
Wenn wir die Rechnung nun für j = 1 , j = 2, …, durchführen erhalten wir die Töne s1,s2,…,die im Intervall [a;a'[liegen. Wegen dem endlichen Tonvorrat müssen 2 Töne identisch sein: sj und sk, für k ≠ j;
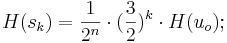
Weil wir definiert haben das 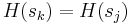 ist, gilt:
ist, gilt:
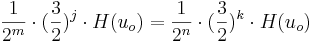
Nun formen wir die Gleichung um:
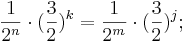
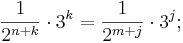
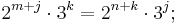
Für Primzahlen 2 und 3 gibt es keine Lösung dieser Gleichung.
Die kanonische Primfaktorzerlegung besagt (aufbauend auf dem Hauptsatz der Arithmetik) , dass jede natürliche Zahl z ≥ 2 eine eindeutig bestimmte Faktorisierung
z = p1n1  p2n2
p2n2  …
…  prns
prns
mit einer natürlichen Zahl s besitzt, Primzahlen
p1 < p2 < … < ps
und natürliche Zahlen n1, n2, …, ns;
Beweisführung oder Primfaktorzerlegung nach Gauß
Daher kann es für die beiden Primzahlen 2 und 3 keine Lösung der Gleichung geben.
Daraus folgt, dass kein Tonsystem sowohl Oktaven- als auch Quinten-vollständig ist.
Da die Quarte das komplementär Intervall zur Quinte ist folgt daraus, dass kein Tonsystem sowohl Quinten- als auch Quarten-vollständig ist.
'weiter zur Erweiterung des Tonsystems
zurück zur Übersichtsseite
- ↑ vgl. Reimer S.17 f.

