12-Ton-System

Erweiterung des 7-Ton Systems:

Deshalb müssen wir die 7-tönige natürliche Tonskala erweitern:

Nehmen wir dafür die Töne

C

D

E

F

G

A

H

(c)

und die eine Oktave höheren Töne:

c

d

e

f

g

a

h

(c')

her. Wie wir aus der Beschreibung der pythagoreischen oder diatonischen Stimmung wissen, kann man nicht zu allen diesen Tönen die Quinte bilden.

Es ist unmöglich die Quinte zu d oder zu h zu bilden.

Wenn wir auf D eine reine Quinte intonieren, so erhalten wir die Tonhöhe: (k stellt den Endton da)

$H(k) = \frac {3}{2} \cdot H(d) = \frac {3}{2} \cdot \frac {9}{8} \cdot H(c) = \frac {27}{16} \cdot H(c)$

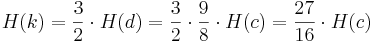
Der Ton muss also etwas über dem a liegen. Das Verhältnis von a können wir aus der Tabelle der Verhältnisse der natürlichen Tonleiter ablesen. Es Beträgt: 5:3.

$\frac {27}{16} - \frac {5}{3} = \frac {1}{48};$

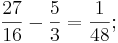
Der Abstand von k zu a wäre also nur 1/48, was viel zu klein wäre.

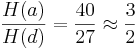$\frac {H(a)}{H(d)} = \frac {40}{27} \approx \frac {3}{2}$ stellt die „unreine“ Quinte da.

Das Verhältnis von unreiner Quinte und reiner Quinte ist:

$\frac {3}{2} : \frac {40}{27} = \frac {81}{80} = 1 + \frac {1}{80};$

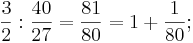
Sie sind also um 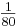$\textstyle \frac {1}{80}$ verschieden, was kaum hörbar ist.

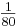($\textstyle \frac {1}{80}$ ist das syntonische Komma)

Nun ist können wir zwar auf d eine Quinte intonieren, auch wenn es eine „unreine“ Quinte ist, aber auf das h kann man immer noch keine Quinte bilden.
Denn dem Intervall h-f entsprechen 3 Ganztonschritte, dem Intervall h-g 4. Die Quinte besteht aber aus 3,5 Ganztonschritten.
Man muss also zwischen dem f und dem g einen Ton einfügen.

'weiter zur Erweiterung des Tonsystems-2

zurück zur Übersichtsseite