Symmetrische Kryptographie

Symmetrische Kryptographie

Aber nun zurück zur Frage von Alice, wie sie ihre E-Mail sicher verschlüsseln kann.
Zunächst sollte man zur Beantwortung der Frage zwei „Arten“ der Verschlüsselung unterscheiden. Eine mögliche Aufteilung der Kryptographie ergibt sich aus der Unterscheidung zwischen symmetrischer Verschlüsselung, die in diesem Lernpfad nur am Rand erwähnt wird und asymmetrischer Verschlüsselung, zu der auch RSA gehört.

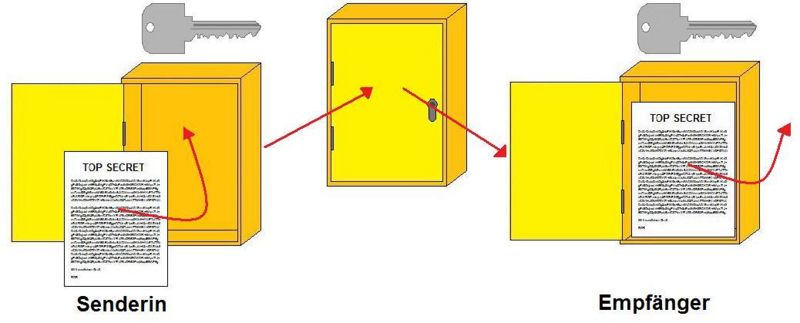
Bei symmetrischen Verschlüsselungen (Private-Key/Secret-Key Kryptographie) handelt es sich um Verfahren, bei denen beide Kommunikationspartner, also sowohl Sender als auch Empfänger der Nachricht, den gleichen Schlüssel zur Ver- bzw. Entschlüsselung des übertragenen Textes verwenden. Ein Schlüssel ist hierbei eine zufällige Ziffernfolge, die die Beteiligten vor dem Gespräch vereinbart haben. Um den Schlüssel sicher auszutauschen, müssten sich Alice und Bob aus unserem Beispiel persönlich treffen, was jedoch aufgrund der großen Entfernung der Wohnorte nicht möglich ist. Diese Schwierigkeit des Schlüsselaustauschs bei symmetrischen Verschlüsselungsverfahren kann als Schlüsselverteilungsproblem bezeichnet werden. Sicher wird nun der eine oder andere offerieren/anbieten, die beiden könnten den Secret Key doch per Telefon oder Brief übermitteln, jedoch ist hierbei einzuwenden, dass der Key dabei in der Regel unverschlüsselt übertragen wird. Bei beiden Übermittlungsmethoden spricht man in einem solchen Fall jeweils von einem unsicheren Kanal, der von Mallory abgehört oder anderweitig eingesehen werden könnte.
Man kann das zwar für übertrieben halten, doch Kryptografen gehen davon aus, dass „Mallory [...] immer gefährlicher [ist], als man denkt.“ [8, S.11]. Die symmetrische Verschlüsselung ist also keine zufriedenstellende Lösung für das Problem von Alice und Bob.

=> Wie Alice und Bob es dennoch schaffen können, ihre E-Mails sicher zu verschlüsseln, erfährst du auf den nächsten Seiten.

zurück zur Übersicht