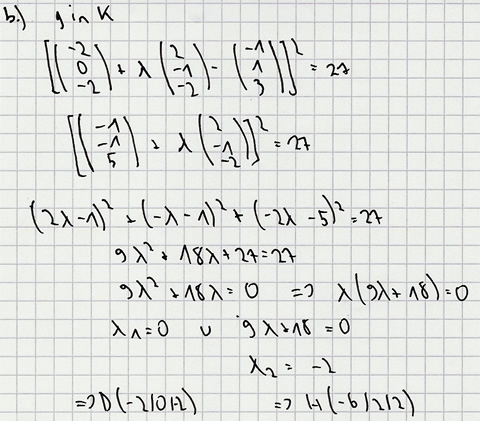- Aufgabe 1
a)Alle Scharebenen haben eine Gerade gemeinsam, die mit g bezeichnet wird. Geben Sie eine Gleichung von g an. 2 BE
- [Lösung anzeigen][Lösung ausblenden]
b) Zeigen Sie, dass Za : 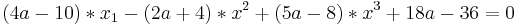 eine weitere mögliche Gleichung für die Ebenenschar Za ist.5 BE eine weitere mögliche Gleichung für die Ebenenschar Za ist.5 BE
- [Lösung anzeigen][Lösung ausblenden]
c) Berechnen Sie, für welchen Wert des Parameters a die zugehörige Scharebene senkrecht auf der Scharebene Z1 steht. 4 BE
- [Lösung anzeigen][Lösung ausblenden]
d) Zeigen Sie, dass die Scharebene Z2 eine winkelhalbierende Ebene der beiden zueinander senkrechten Scharebenen Z1 und Z4 ist. 5 BE
- Vorlage:Lösung 1 versteckt
- Vorlage:Lösung 2 versteckt
- Aufgabe 2
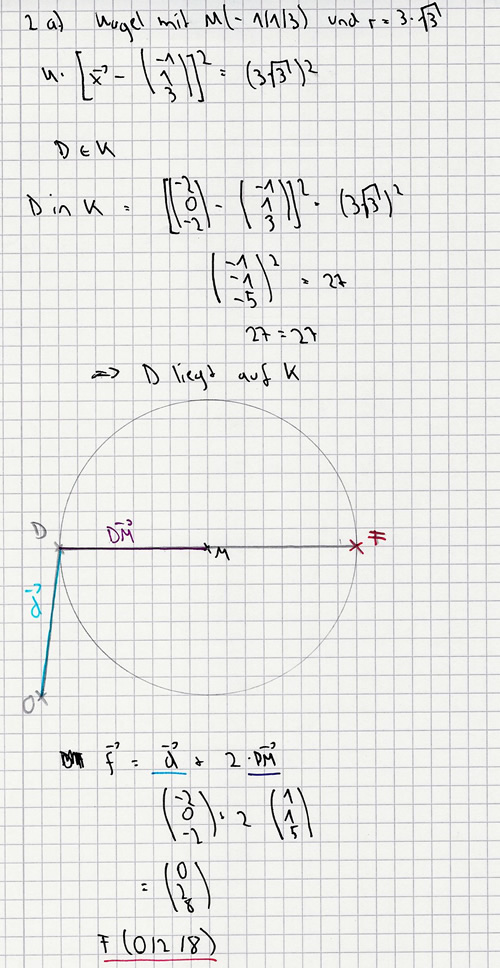
Der Punkt M(-1| 1 | 3) ist Mittelpunkt einer Kugel mit Radius ![\sqrt[3]{3}](/images/math/6/8/1/681d3d042b97f0fd1136ccaf260a53e5.png) . .
a)Zeigen Sie, dass der Punkt D auf dieser Kugel liegt, und berechnen Sie die Koordinaten des Kugelpunkts F, für den [FD] ein Durchmesser der Kugel ist. [Ergebnis: F(0 | 2 | 8)] 4 BE
- [Lösung anzeigen][Lösung ausblenden]
b) Bestimmen Sie die Koordinaten der Kugelpunkte, die auf der Geradeng liegen. [Ergebnis: D und H(-6 | 2 | 2) ] 6 BE
- [Lösung anzeigen][Lösung ausblenden]
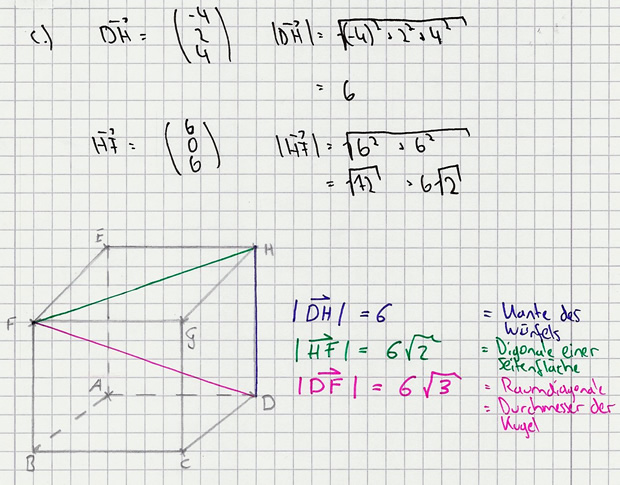
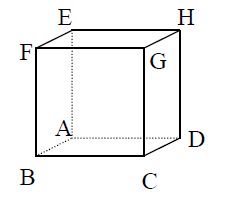
c) Berechnen Sie die Längen DH und HF und begründen Sie, dass man die drei Punkte D, F und H zu einem Würfel ABCDEFGH wie in der Abbildung ergänzen kann. 6 BE
- [Lösung anzeigen][Lösung ausblenden]
|
 |
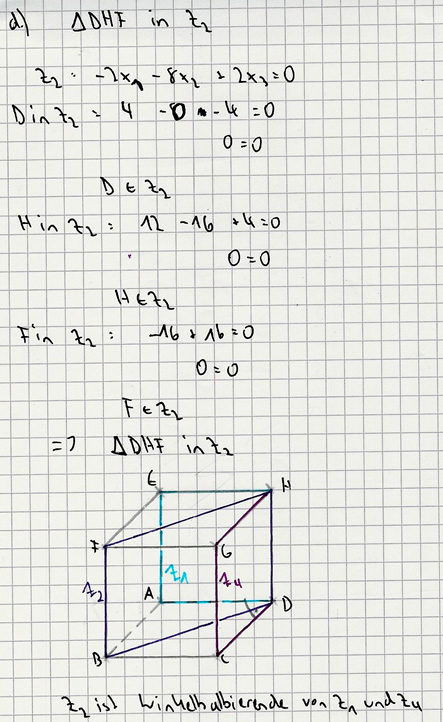
d) Zeigen Sie, dass das Dreieck DHF in der Ebene Z2 liegt. Begründen Sie ohne Rechnung nur mit Hilfe der bisherigen Ergebnisse, warum
die Ebenen Z1 und Z4 je eine Würfelfläche enthalten. 5 BE
- [Lösung anzeigen][Lösung ausblenden]
e) Der Eckpunkt G liegt in Z4 (Nachweis nicht erforderlich). Berechnen Sie die Koordinaten von G. 4 BE
- [Lösung anzeigen][Lösung ausblenden]
| 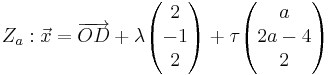 mit D (-2 | 0 | -2) und λ, τ, a є IR.
mit D (-2 | 0 | -2) und λ, τ, a є IR.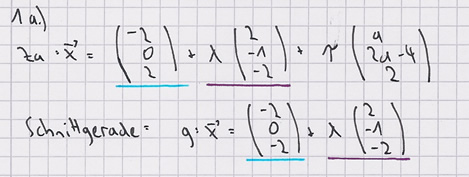
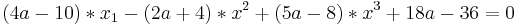 eine weitere mögliche Gleichung für die Ebenenschar Za ist.5 BE
eine weitere mögliche Gleichung für die Ebenenschar Za ist.5 BE
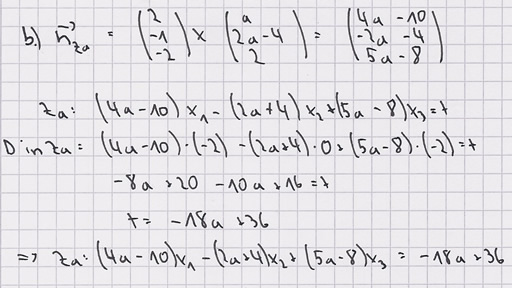

![\sqrt[3]{3}](/images/math/6/8/1/681d3d042b97f0fd1136ccaf260a53e5.png) .
.