2004 II
|
|
Gegeben ist die Funktion
a) Berechnen Sie die Nullstelle von f und untersuchen Sie das Verhalten von f an den Rändern von Df.
[[Bild:]]
[[Bild:]]
[[Bild:]]
|
Zwei Gänge von 2,0 m und 4,0 m Breite treffen rechtwinklig aufeinander. Es soll die größtmögliche Länge L eines Balkens ermittelt werden, den man in horizontaler Lage aus einem Gang in den anderen tragen kann. Die Dicke des Balkens wird als vernachlässigbar klein angesehen.
[[Bild:]]
[[Bild:]]
|
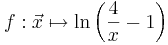 mit dem maximalen Definitionsbereich Df = ]0;4[. Der Graph von f wird mit Gf bezeichnet.
mit dem maximalen Definitionsbereich Df = ]0;4[. Der Graph von f wird mit Gf bezeichnet.
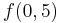 . Zeichnen Sie Gf unter Berücksichtigung der bisherigen Ergebnisse. Zeichnen Sie auch die Tangente im Symmetriezentrum ein (Ursprung des Koordinatensystems in der Blattmitte).
. Zeichnen Sie Gf unter Berücksichtigung der bisherigen Ergebnisse. Zeichnen Sie auch die Tangente im Symmetriezentrum ein (Ursprung des Koordinatensystems in der Blattmitte).
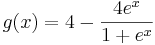 . Tragen Sie den Graphen von g in das Koordinatensystem der Teilaufgabe 1d ein.
. Tragen Sie den Graphen von g in das Koordinatensystem der Teilaufgabe 1d ein.
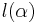 ist die Maßzahl der in Meter angegebenen Länge der Strecke [AB] und definiert für 0° <
ist die Maßzahl der in Meter angegebenen Länge der Strecke [AB] und definiert für 0° <  < 90° die Funktion
< 90° die Funktion 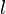 .
.
 .
.

