Abi 2014 Geometrie I Teil B
|
|
|
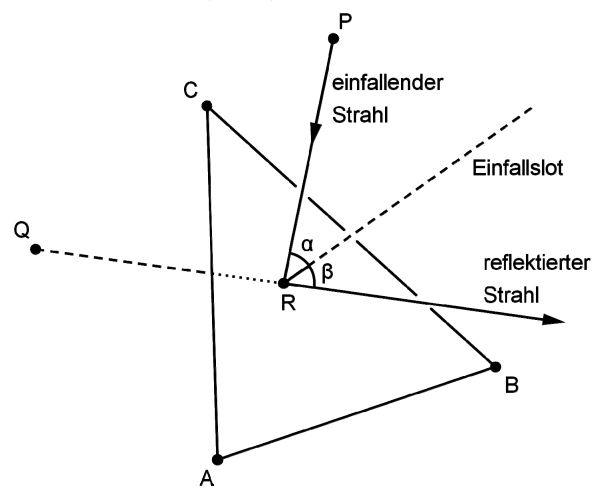
In einem kartesischen Koordinatensystem legen die Punkte A(4|0|0), B(0|4|0) und C(0|0|4) das Dreieck ABC fest, das in der Ebene E:x1+x2+x3=4 liegt. a) Bestimmen Sie den Flächeninhalt des Dreiecks ABC. Das Dreieck ABC stellt modellhaft einen Spiegel dar. Der Punkt P(2|2|3) gibt im Modell die Position einer Lichtquelle an, von der ein Lichtstrahl ausgeht. Die Richtung dieses Lichtstrahls wird im Modell durch den Vektor b) Geben Sie eine Gleichung der Geraden g an, entlang derer der Lichtstrahl im Modell verläuft. Bestimmen Sie die Koordinaten des Punkts R, in dem g die Ebene E schneidet, und begründen Sie, dass der Lichtstrahl auf dem dreieckigen Spiegel auftrifft. (zur Kontrolle: R(1,5|1,5|1)) Der einfallende Lichtstrahl wird in demjenigen Punkt des Spiegels reflektiert, der im Modell durch den Punkt R dargestellt wird. Der reflektierte Lichtstrahl geht für einen Beobachter scheinbar von einer Lichtquelle aus, deren Position im Modell durch den Punkt Q(0|0|1) beschrieben wird (vgl. Abbildung). c) Zeigen Sie, dass die Punkte P und Q bezüglich der Ebene E symmetrisch sind. Das Lot zur Ebene E im Punkt R wird als Einfallslot bezeichnet. d) Die beiden Geraden, entlang derer der einfallende und der reflektierte Lichtstrahl im Modell verlaufen, liegen in einer Ebene F. Ermitteln Sie eine Gleichung von F in Normalenform. Weisen Sie nach, dass das Einfallslot ebenfalls in der Ebene F liegt. (mögliches Teilergebnis: F:x1-x2=0) e) Zeigen Sie, dass die Größe des Winkels β zwischen reflektiertem Lichtstrahl und Einfallslot mit der Größe des Winkels α zwischen einfallendem Lichtstrahl und Einfallslot übereinstimmt.
|
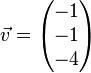 beschrieben.
beschrieben.