Volumenänderung bei Temperaturänderung
Volumenänderung von Flüssigkeiten
(Daniel H.<-Hat alles alleine gemacht,Patrik H.,Sebastian B.,Christoph Z.)
Flüssigkeiten (ausser Wasser) dehnen sich bei konstanter Temperaturerhöhung linear aus.
Volumenausdehnung = Ausgangsvolumen * Volumenausdehnungskoeffizient * Temperaturdifferenz
Volumenausdehnungskoeffizienten Beispiele (γ in 10-3/K bei 20 °C):
Benzin: 1,06
Quecksilber: 0,182
Petroleum: 0,96
Mineralöl: 0,70
Beispiel:
Berechne die Volumenänderung von 76 LiterBenzin wenn sie sich von 10°C auf 20°C erwärmen
Gegeben:
V1=76l γ=1,06 ^T=10°C
Längenänderung von Festkörpern
Alle Festkörper dehnen sich bei Erwärmung aus, jedoch nicht alle gleichmäßig (linear). Dafür ist der jeweilige Längenausdehnungskoeffizient verantwortlich. Dieser ist bei jedem Stoff anders. Es kann berechnet werden, um wie viel cm sich ein Stoff ausdehnt und zwar mit dieser Formel:
Δl = α * lo * Δδ
oder:
Volumenänderung = Volumenänderugskoeffizient * Ausgangslänge * Temperaturänderung
Einige Beispiele für den Längenausdehnungskoeffizient:
| Stoffe
|
α = 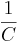
|
|
Stoffe
|
α = 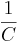
|
| Elemente
|
|
|
Andere
|
|
| Aluminium
|
2,4 * 10-5
|
|
Beton
|
0,000 012
|
| Messing
|
0,000 018
|
|
Glas
|
0,000 008
|
| Silber
|
0,000 020
|
|
Granit
|
0,000 003
|
| Gold
|
0,000 014
|
|
Kochsalz
|
0,000 040
|
| Zinn
|
0,000 027
|
|
Polyester
|
0,000 080
|
| Zink
|
0,000 036
|
|
PVC (biegsam)
|
0,000 240
|
| Kupfer
|
0,000 016
|
|
Porzellan
|
0,000 003
|
| Blei
|
0,000 029
|
|
Titan
|
0,000 010
|
| Eisen
|
0,000 012
|
|
Silizium
|
0,000 002
|
Anomalie des Wassers
|
Dichte:
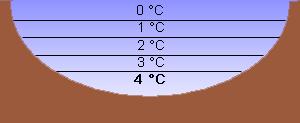
Wasser hat unter Normaldruck seine größte Dichte von bei ca. 4°C und zeigt damit eine Dichteanomalie.
Diese besteht darin, dass sich Wasser unterhalb von ca. 4°C bei weiterer Temperaturverringerung, auch beim Wechsel zum festen Aggregatzustand, wieder ausdehnt, was man nur von wenigen Stoffen kennt.
Dies führt dazu, dass Eisberge schwimmen.
Im flüssigen Zustand herrscht eine Mischung von Ordnung und Chaos, wobei die Moleküle aufgrund ihrer höheren Geschwindigkeit ein größeres Volumen ausfüllen.
Es erhöht sich also das Volumen und die Dichte wird damit geringer.
Im gasförmigen Zustand ist die maximale Unordnung erreicht und die Atome verteilen sich dementsprechend gleichmäßig über den maximal zur Verfügung stehenden Raum.
Festes Wasser hat eine geringere Dichte als flüssiges Wasser, es schwimmt (anomales Verhalten)
Es gilt:
-je größer die Temperatur des Wassers, desto kleiner die Dichte
-je kleiner die Temperatur des Wassers, desto größer die Dichte
Außer:
Ab 4°C wird das Volumen nicht kleiner sondern bis 0°C wieder größer.
Wasser hat bei 4°C die größte Dichte.
|
Elektrische Energie
Ladung, Stromstärke, Spannung
Ladung Q
- Körper bzw. Teilchen können elektrisch neutral, positiv oder negativ geladen sein.
- Die elektrische Ladung Q eines Körpers bzw. Teilchens gibt an, wie groß der Elektronenmangel oder -überschuss ist.
|
1C = 1As
1C (Coulomb)
1As (Amperesekunde)
|
- Dei Ladung eines Elektrons wird als Elementarladung e bezeichnet.
Stromstärke I
Sie gibt an, wie viel Ladung in einer bestimmten Zeit durch einen Leiterquerschnitt fließt.
Die Stromstärke kann man mit einem Amperemeter messen. Das Gerät wird in den Stromkreis geschaltet!
Wenn I konstant ist gilt:
|
I = Q/t
Stromstärke = Ladung pro Zeit
|
Spannung U
Sie gibt an, wie stark der Antrieb des elektrischen Stroms ist.
Die Spannung kann man mit einem Voltmeter messen. Das Gerät muss parallel geschaltet werden!
Bei der Spannung gilt:
|
U =  E/Q E/Q
|
|
Widerstände in Stromkreisen
Welcher Strom in einem Stromkreis fließt, hängt einerseits von der elektrischen Spannung der Batterie ab, andererseits aber auch vom eingesetzten Verbraucher, genauer gesagt von seinem elektrischen Widerstand. Der Widerstand ist eine Eigenschaft des Verbrauchers, die man als seine Fähigkeit umschreiben kann, die schnelle Bewegung der elektrischen Ladung zu behindern. Mehr Widerstand bedeutet also bei gleicher Spannung, dass weniger Strom fließt. Der Widerstand R ist als abgeleitete Größe aus Spannung U und Stromstärke I definiert.
Die Einheit des elektrischen Widerstands ist Ohm. Ein Ohm ist gleich ein Volt geteilt durch ein Ampere. Der Widerstand einer Glühlampe mit U=6V und I=0,4A kann also leicht berechnet werden:
R = U/I
R = 6V/0,4A
R = 15 Ohm
|
Elektrische Energie und elektrische Leistung
|
|
|
|
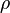 *g*h
*g*h


 E/Q
E/Q

