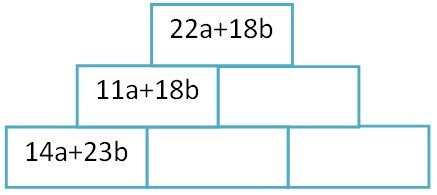
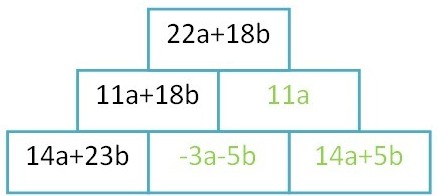
Auflösen von Klammern

Klammerregeln bei Addition und Subtraktion

Aufgabenstellung:

Überlege, wie du die Klammern auflösen kannst.

T(x;y)= 9x+(8x+5y)
T(x;y)= 9x+(8x-5y)
T(x;y)= 9x-(8x+5y)
T(x;y)= 9x-(8x-5y)

Lösung anzeigen

Erklärung:

Farbig

Steht vor der Klammer ein Pluszeichen, so kann man die Klammer weglassen, ohne dass sich der Wert des Terms ändert.

a+(b+c) = a+b+c

a+(b-c) = a+b-c

Steht vor der Klammer ein Minuszeichen, so wird beim Auflösen der Klammer aus jedem Pluszeichen in der Klammer ein Minuszeichen und aus jedem Minuszeichen in der Klammer ein Pluszeichen.

a-(b+c) = a-b-c

a-(b-c) = a-b+c

Beispiel:

2x²+36x+(34x-11) = 2x²+36x+34x-11 = 2x²+70x-11
Vereinfache selbst:

19y-(20y-18)
5z+(7z-3+2z)

Lösung anzeigen

Übungsaufgaben

Aufgabe 1:Vereinfache so weit wie möglich:

36a-(12a+9)
27n+(-5n+4)
29m-(3-m)
8x+(9-x)

Lösung anzeigen

Aufgabe 2:

Schreibe die Summe (a-b)+(x-y) als Differenz
Schreibe die Differenz (m-l)-(z-u) als Summe

Lösung anzeigen

Aufgabe 3:

Finde die fehlenden Zeichen (O) und Termglieder(Fehler beim Parsen(Unbekannte Funktion „\box“): \box )

(Fehler beim Parsen(Unbekannte Funktion „\box“): \box

n +2y) - (4n O 17y) = 6n+19y

(2n O 3m) + (Fehler beim Parsen(Unbekannte Funktion „\box“): \box

n - Fehler beim Parsen(Unbekannte Funktion „\box“): \box m) = 7n-10m

(13a O Fehler beim Parsen(Unbekannte Funktion „\box“): \box

b) - (Fehler beim Parsen(Unbekannte Funktion „\box“): \box a+5b) = 4a+4b

Lösung anzeigen

Aufgabe 4:


Bei dieser Termmauer steht auf jedem Stein die Summe der Terme, die auf den beiden Steinen darunter stehen. Übertrage die Zeichnung in dein Heft und vervollständige sie.