reine Stimmung1
Quint-Terz System (reine Stimmung)
Da die pythagoreische Stimmung, wie oben beschrieben, v.a. in der Mehrstimmigkeit Probleme hatte, musste ein anders System entwickelt werden.
Man setzt nun neben Quinte und Oktave auch die (große) Terz fest. Und zwar, statt sie aus den gestapelten Quinten, wie die Pythagoreer, zu berechnen, teilte man eine Saite in 5 Teile und erhielt das Verhältnis 5:4 und berechnete ausgehend von den 3 Basisintervallen die restlichen Intervalle. Die reine Stimmung wird auch als diatonische und als natürliche Stimmung bezeichnet.
Da die Stimmung auf den 3 Intervallen Quinte, Terz und Oktave basiert, heißt sie Quint-Terz Stimmung.
Deshalb ist eine Möglichkeit, diese Stimmung darzustellen, die Darstellung als Vektoren.
(1) Die Oktave, in Vektorform Ok= [ 1 0 0] (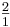 )
)
(2) Die Quinte, in Vektorform Q = [ 0 1 0] (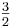 )
)
(3) Die große Terz, in Vektorform gT = [ 0 0 1] (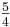 )
)
Axiom: Man kann keines der Grundintervalle als Linearkombination
der übrigen beiden darstellen.
Axiom: Jedes Intervall kann als Summe oder Differenz dieser drei
Grundintervalle geschreiben werden.
Vektorschreibweise: i=[ x y z ]= x·Ok + y·Q + z·gT
x,y,z 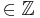
[x y z] werden als Oktav-Quint-Terz-Vektor bezeichnet.
Die Basisintervalle können ersetzt werden durch folgende drei
Basisintervalle.
(1) Großer Ganzton G, als Vektor (100) = [-1 2 0] (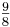 )
)
(2) kleiner Ganzton G-, als Vektor (010) = [ 1 -2 1] (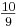 )
)
(3) Halbton H, als Vektor (001) = [ 1 -1 -1] (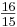 )
)
Umrechnung:
| Oktave Ok = (322) |
| Quinte Q = (211) |
| Terz gT = (110) |
Oder durch folgende drei Basisintervalle (Halbtöne + Korrektur)
(1) Halbton H H = {100} = (001) = [1 -1 -1] (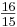 )
)
(2) synt. Komma K = {010} = (1 -1 0) = [-2 4 -1] (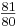 ) (21,51 Cent)
) (21,51 Cent)
(3) 2H-G k = {001} = (-1 0 2) = [3 -4 -2] (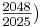 [1]
[1]
Beispiel: Wie wird die Septime c-h aus Oktaven, Quinten und Terzen zusammengesetzt?
c-d-e-f-g-h: G + (G-) + H + G + (G-) + G
Als (G,G-,H)-Vektor = (Anzahl von G und G- und H) geschrieben: c - h = (3 2 1)
"Zwei große Ganztöne, ein kleiner Ganzton und zwei Halbtöne".
Vektorrechnung:
(3 2 1) = 3·(1 0 0) + 2·(0 1 0) + 1·(0 0 1) = 3·[-1 2 0] + 2·[1 -2 1] + 1·[1 -1 -1] = [0 1 1] = "Eine Quinte + eine große Terz"
c-h umfasst 11 Halbtöne(c-des-d-es-e-f-fis-g-as-a-b-h).
Das Problem ist, dass es keine gleichen Halbtöne sind. Nun muss man noch die "Korrekturen" K = {0 1 0} (synt. Komma) und k = {0 0 1} (Ganzton - 2 Halbtöne) vornehmen.
Das Ergebnis {x y z} erhält man durch Lösen der Gleichung:
{x y z} = x·(0 0 1) + y·(1 -1 0) + z·(-1 0 2) = (3 2 1)
Das lineares Gleichungssystem
(I) y - z = 3 (II) -y = 2 (III) x + 2·z = 1
aus (II) folgt: y = -2;
(II) in (I):
-2 – z = 3; z = -5;
z in (III):
x + 2*(-5) ) = 1; x = 11
hat die Lösung: {x y z} = {11 -2 -5), d.h. c-h liegt 11 Halbtöne auseinander. Der Ton ist jedoch zu hoch. Zur Korrektur muss man zwei synth. Komma und 5 mal die (Differenz von zwei Halbtönen und Ganzton) tiefer.
Auf diese Art lassen sich alle Intervalle der reinen Stimmung darstellen.
zurück zur reinen Stimmung
zurück zur Übersichtsseite
- ↑ vgl. http://delphi.zsg-rottenburg.de/axiomensystem.html [Stand 2010-11-29]

