temperierte Stimmung
Die Gleichstufig temperierte Stimmung:
Es wurde eine Tonskala postuliert, die für den j-ten Ton 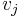 , mit 2 noch zu bestimmenden Konstanten k und l folgende Gleichung erfüllt:
, mit 2 noch zu bestimmenden Konstanten k und l folgende Gleichung erfüllt:
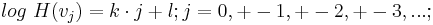
Des weiteren sollte folgendes gelten: 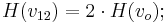 da man die Oktave in 12 Halbtonschritte einteilen wollte. Deshalb gitl für l:
da man die Oktave in 12 Halbtonschritte einteilen wollte. Deshalb gitl für l:
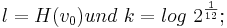
Daraus erhält man die Formel zu Berechnung aller Töne in der gleichstufig temperierten Skala:
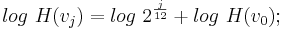
wenn man nun substituiert mit q := 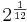 erhält man:
erhält man:
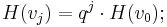 j = 0, +-1,+-2,+-3, …[1]
j = 0, +-1,+-2,+-3, …[1]
Es war also nun ein Kompromiss nötig: man verzichtete etwas auf die Reinheit der Intervalle und schuf dafür Intervalle mit gleichen Abständen, unabhängig von Tonarten. Jeder Halbton sollte als das gleich Frequenzverhältnis haben.
Um die Oktavspanne in 12 gleich große Töne aufzuteilen, ergibt sich für jeden Halbtonschritt:
![\textstyle \sqrt[12] {2}](/images/math/7/c/b/7cbac490f275a9c3a2e5128ca2f3f852.png) oder
oder 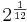 , was einem Wert von 1,05946 entspricht.
, was einem Wert von 1,05946 entspricht.
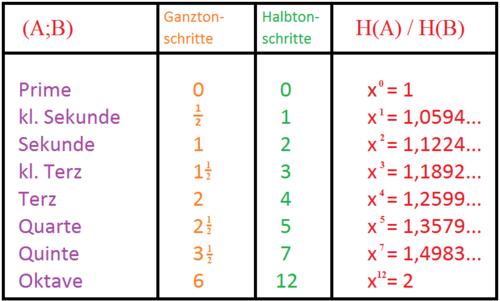
Daraus folgt für die (wichtigsten) Intervalle bei beliebiger Wahl des Grundtons  :
A und B sind 2 Variablen für beliebige Töne und geben nicht die beiden Töne a und b wieder.
:
A und B sind 2 Variablen für beliebige Töne und geben nicht die beiden Töne a und b wieder.
X ist nicht transzendent, sondern algebraisch.
Die algebraische Gleichung lautet:
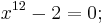
Allerdings wird die Quinte, die vorher durch die rationale Zahl 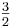 dargestellt war als unreine Quinte durch die irrationale Zahl
dargestellt war als unreine Quinte durch die irrationale Zahl 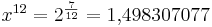 .... wiedergegeben.
.... wiedergegeben.
Die Gleichheit cis = des, dis = es, … wird in der Musik als enharmonische Verwechslung beziechnet.
Alle Intervalle (außer die Oktave) sind nun unrein, d.h. sie sind nicht schwebungsfrei (alle Quinten sind zu tief, alle Quarten zu hoch).
Der Vorteil des Systems ist jedoch, das endlich ein System geschaffen wurde, das geschlossen ist und in dem alle Tonarten spielbar sind.
Die gleichstufig temperierte Stimmung ist eine geschlossene Temperatur, da sich der Quintenzirkel nach der 12. Quinte schließt und nicht, wie z.b. bei der (groß-Terz) mitteltönigen Stimmung nach der 12. Quinte eine sogenannte Wolfsquinte entsteht.
weiter zum Vergleich der Stimmungen
zurück zur Übersichtsseite
- ↑ vgl. Reimer S.27

