2008 VI
Aus RMG-Wiki
< LK Mathematik | Abitur
Version vom 5. Februar 2010, 12:09 Uhr von Gehrig Melissa (Diskussion | Beiträge)
|
|
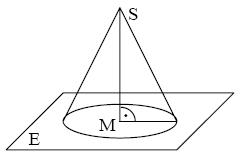
In einem kartesischen Koordinatensystem des IR3 sind die Punkte M(−2|4|1), S(6|8|9), P(4|−8|1) sowie die Gerade g : a) Ermitteln Sie eine Gleichung der Ebene E in Normalenform und zeigen Sie, dass der Punkt P auf dem Grundkreis k liegt.
|
|
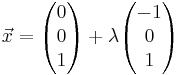 , λ ∈ IR gegeben.
Die Strecke [MS] ist die Höhe eines geraden Kreiskegels. Sein Grundkreis k um den Punkt M hat den Radius
, λ ∈ IR gegeben.
Die Strecke [MS] ist die Höhe eines geraden Kreiskegels. Sein Grundkreis k um den Punkt M hat den Radius 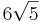 und liegt in der Ebene E.
und liegt in der Ebene E.