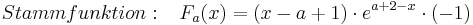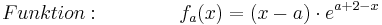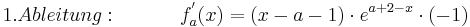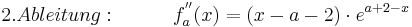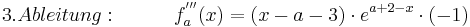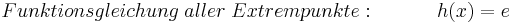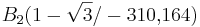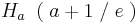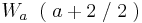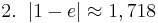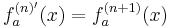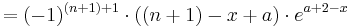Lösungsübersicht

Funktion

$Stammfunktion: \;\;\; F_a (x) = ( x - a + 1 )\cdot e^{a + 2 - x}\cdot (-1)$

$Funktion: \;\;\;\;\;\;\;\;\;\;\;\;\;\; f_a (x) = ( x - a )\cdot e^{a + 2 - x}$

$1. Ableitung: \;\;\;\;\;\;\;\; \;\;\; f^{'}_a (x) = ( x - a - 1 )\cdot e^{a + 2 - x}\cdot (-1)$

$2. Ableitung: \;\;\;\; \;\;\;\;\;\;f^{''}_a (x) = ( x - a - 2 )\cdot e^{a + 2 - x}$

$3. Ableitung: \;\;\;\;\;\;\;\;\;\; f^{'''}_a (x) = ( x - a - 3 )\cdot e^{a + 2 - x}\cdot (-1)$

Der Graph von 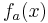$f_a(x)\,$

Teilaufgabe a)

$Nullstelle: \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;NS \; ( \;a\;/ \;0 \;)\;$

$Schnittpunkt\; mit \;der\; y-Achse: \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;SP_{y-Achse} \;( \;0 \;/\; -a \cdot e^{a+2}\;)\;$

$Extrempunkt:\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; Max \; (\; 1 + a \;/\; e\; )\;$

$Wendepunkt: \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; WP \; (\; a + 2 \;/ \;2 \;)\;$

$Funktionsgleichung\; aller\; Extrempunkte: \;\;\;\;\;\;\;\;\;\;\; h (x) = e\;$

Teilaufgabe b)

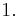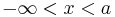$1.\;$ Für $-\infty < x < a$ ist der G_Fa streng monoton fallend.

Für 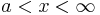$a < x < \infty$ ist der G_Fa streng monoton steigend.

Für $x = a\;$ besitzt G_Fa einen Tiefpunkt.

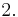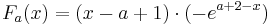
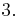$2.\;$ Stammfunktion: $F_a (x) = ( x - a + 1 )\cdot (-e^{a + 2 - x})$

$3.\;$ Flächeninhalt zwischen der x-Achse und dem Graphen der Funktion f₂: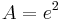 $A = e^{2}\;$

Teilaufgabe c)

$1.\;\;a = 2008\;$

$2.\;\;B_1(1 + \sqrt{3} / 2{,}601)$

$\;\;\;\;\;\;\; B_2(1 - \sqrt{3} / -310{,}164)$

Teilaufgabe d)

$1.\;\;R_a \;\;(\; a\; /\; 0\; )\;$

$H_a \;\;(\; a + 1 \;/\; e\; )\;$

$W_a \;\;(\; a + 2 \;/\; 2 \;)\;$

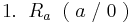
Da sich die y-Werte dieser Punkte nicht verändern, haben diese immer denselben Abstand
zueinander. Deshalb sind alle Dreiecke, die durch diese Punkte festgelegt sind, kongruent.

$2. \;\;| 1 - e | \approx 1,718$

Teilaufgabe e)

$f_a^{(n)'}(x)= f_a^{(n+1)}(x)$

$=(-1)^{(n+1)+1}\cdot((n+1)-x+a)\cdot e^{a+2-x}$

--Andre Etzel 23:18, 22. Jan. 2010 (UTC)