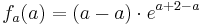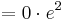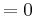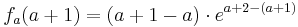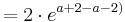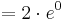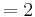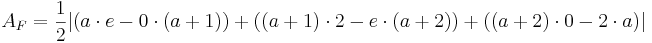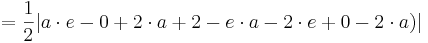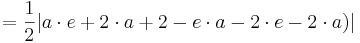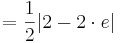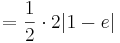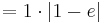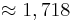Lösung von Teilaufgabe d

Kongruenz der Dreiecke

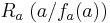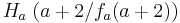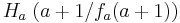Die Dreiecke werden durch die Punkte $\; R_a\;( a / f_a (a))$, $H_a\; ( a + 2 / f_a ( a + 2 ))$ und $H_a\; ( a + 1 / f_a ( a + 1 ))$ festgelegt.

1.Punkt : 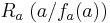$\; R_a\;( a / f_a (a))$

$f_a (a) = ( a - a )\cdot e^{ a + 2 - a }$

$= 0\cdot e^{ 2 }$

$= 0\;$

Der Punkt R_a liegt für alle a bei R_a ( a / 0 )

2.Punkt : 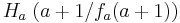$H_a\; ( a + 1 / f_a ( a + 1 ))$

$f_a (a+1) = ( a + 1 - a )\cdot e^{ a + 2 - (a+1) }$

$= 1 \cdot e^{ a + 2 - a-1) }$

$= 1 \cdot e^{1}$

$= e\;$

Der Punkt H_a liegt für alle a bei H_a ( a + 1 / e )

3.Punkt : 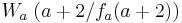$W_a\;( a + 2 / f_a ( a + 2 ))$

$f_a (a+2) = ( a + 2 - a )\cdot e^{ a + 2 - (a+2) }$

$= 2 \cdot e^{ a + 2 - a-2) }$

$= 2 \cdot e^{0}$

$= 2 \;$

Der Punkt W_a liegt für alle a bei W_a ( a + 2 / 2 )

Mit den drei bestimmten Punkten R_a, H_a und W_a lässt sich erkennen, dass die Dreiecke für alle verschiedene a kongruent sind. Die y-Werte aller drei Punkte sind für alle a identisch. Daraus schließt man, dass sich die drei Punkte nur auf der x-Achse beziehungsweise auf einer Parallelen zur x-Achse, immer um den gleichen Wert, nämlich um a, verschieben. Da sich die Punkte nur auf Parallelen zur x-Achse verschieben, heißt das natürlich auch, dass sich das Dreieck nur auf der x-Achse verschiebt und somit immer kongruent ist.

Flächeninhalt des Dreiecks

Der Flächeninhalt eines Dreiecks im zweidimensionalen Raum beträgt nach der Formelsammlung (Mathematische Formeln und Definitionen von Barth, Mühlbauer, Nikol, Wörle) auf Seite 81:

$im R^{2}: A = \frac{1}{2} | ( a_1\cdot b_2 - a_2\cdot b_1) + ( b_1\cdot c_2 - b_2\cdot c_1 ) + ( c_1\cdot a_2 - c_1\cdot a_2 ) |$

$Definiere: \;$
$A\; (\;a_1 \;/\; a_2 \;) = R_a \;(\; a \;/\; 0\; )$
$B\; (\;b_1 \;/\; b_2 \;) = H_a \;( \;a + 1\; /\; e \;)$
$C\; (\;c_1 \;/\; c_2 \;) = W_a \;(\; a + 2 \;/ \;2 \;)$

$A_F = \frac{1}{2} | ( a\cdot e - 0\cdot (a+1)) + ( (a+1)\cdot 2 - e\cdot (a+2) ) + ( (a+2)\cdot 0 - 2\cdot a ) |$

$= \frac{1}{2} | a\cdot e - 0 + 2\cdot a + 2- e\cdot a -2\cdot e + 0 - 2\cdot a ) |$

$= \frac{1}{2} | a\cdot e + 2\cdot a + 2- e\cdot a -2\cdot e - 2\cdot a ) |$

$= \frac{1}{2} | 2 -2\cdot e |$

$= \frac{1}{2}\cdot2 | 1 - e |$

$= 1\cdot | 1 - e |$

$= | 1 - e |\;$

$\approx 1,718$

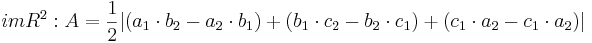
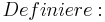
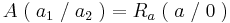
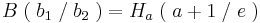
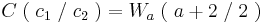
Der Flächeninhalt beträgt, unabhängig von a, | 1 - e |

Grafik zur Kongruenz und zum Flächeninhalt der Dreiecke

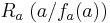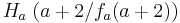
1. In der Graphik lässt sich deutlich erkennen, das die Dreiecke, bestehend aus den Punkten $\; R_a\;( a / f_a (a))$, $H_a\; ( a + 2 / f_a ( a + 2 ))$
und 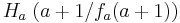$H_a\; ( a + 1 / f_a ( a + 1 ))$ für alle a kongruent (dekungsgleich) sind.
2. Aus erstens folgt zwangsweise auch, dass der Flächeninhalt für alle a gleich groß bleibt. Dies lässt sich auch deutlich in der Graphik erkennen.