HA: Unterschied zwischen den Versionen
Aus RMG-Wiki
(→Aufgabe 2) |
|||
| Zeile 1: | Zeile 1: | ||
| − | + | [[LK Mathematik 2008 10/Lösungen Infi|Lösungen Infi 9.10.2008]] | |
| − | + | ||
| + | [[LK Mathematik 2008 10/Lösungen Infinitesimalrechnung|Lösungen Infinitesimalrechnung 6.10.2008]] | ||
| + | [[LK Mathematik 2008 10/Lösungen Inifi UNterricht|Lösungen Infitesimalrechnen im Unterricht 6.10.2008]] | ||
| + | == Hausaufgabe 6.10.2008== | ||
| + | ;Aufgabe 1 | ||
'''1.Bestimmen der Schnittpunkte:''' | '''1.Bestimmen der Schnittpunkte:''' | ||
Version vom 11. Oktober 2008, 07:19 Uhr
Lösungen Infinitesimalrechnung 6.10.2008
Lösungen Infitesimalrechnen im Unterricht 6.10.2008
Hausaufgabe 6.10.2008
- Aufgabe 1
1.Bestimmen der Schnittpunkte:
f(x)=0;
a * x - b * x3 = 0;
x (a - b * x2)=0
--> Mitternachtsformel: x1= 0; x2=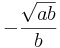 
; x3=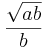 
2.Berechnung des Integrals:
F(x)=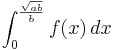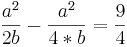
= ... =
I.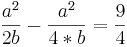
II. f´(1) = 0 ; a - 3b = 0; a = 3b eingesetzt in I.: b = 1 → a = 3
Aufgabe 2
Die Parabel y = -1/4 x2 + 2x schließt mit der y-Achse und der Tangente im Kurvenpunkt P(6,?) ein Flächenstück vollstandig ein. Wie groß ist diese Fläche?
