Benutzer:Scheller Michael: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 1: | Zeile 1: | ||
*'''Von Philipp Issle übernommen!!!''' | *'''Von Philipp Issle übernommen!!!''' | ||
| − | *von: LK Mathematik 2008 10/Lösungen Stochastik | + | *von: LK Mathematik 2008 10/Lösungen Stochastik [http://wikis.zum.de/rmg/index.php/LK_Mathematik_2008_10/L%C3%B6sungen_Stochastik Link-Text] |
*Mit dem Ziel der Verbesserung der Aufgabe 7 | *Mit dem Ziel der Verbesserung der Aufgabe 7 | ||
| Zeile 7: | Zeile 7: | ||
=== Zu Aufgabe 7 === | === Zu Aufgabe 7 === | ||
| − | *In einer Urne befinden sich fünf von 1 bis 5 nummerierte Kugeln! Es werden | + | *In einer Urne befinden sich fünf von 1 bis 5 nummerierte Kugeln! Es werden |
| − | + | a) 2 Kugeln nacheinander ohne zurücklegen gezogen | |
| − | a) nacheinander ohne zurücklegen | + | |
*Möglicher Ergebnissraum wäre dann '''Ω''' = {12,13,14,15,23,24,25,34,35,45}; | *Möglicher Ergebnissraum wäre dann '''Ω''' = {12,13,14,15,23,24,25,34,35,45}; | ||
| Zeile 17: | Zeile 16: | ||
*Mächtigkeit ist '''|Ω|'''= '''4+3+2+1=10''' | *Mächtigkeit ist '''|Ω|'''= '''4+3+2+1=10''' | ||
| − | b) | + | b) 3 Kugeln gleichzeitig gezogen |
| − | Splitten wir es mal auf und tuen so, als ob jede Kugel einzeln gezogen wird jedoch nicht mehr | + | Splitten wir es mal auf und tuen so, als ob jede Kugel einzeln gezogen wird jedoch nicht mehr zurückgelegt wird. Dann gibt es am Anfang mit dem Zug der ersten Kugel 6 Möglichkeiten, bei der zweiten Kugel 3 Möglichkeiten und bei der dritten Kugel nur 1 Möglichkeit. |
*Möglicher Ergebnissraum wäre dann '''Ω''' = {123,124,125,134,135,145,234,235,245,345} | *Möglicher Ergebnissraum wäre dann '''Ω''' = {123,124,125,134,135,145,234,235,245,345} | ||
| − | *Mächtigkeit ist '''|Ω|'''= ''' | + | *Mächtigkeit ist '''|Ω|'''= '''6+3+1=10''' |
| − | + | ||
[[Bild:Stochastik9.png]] | [[Bild:Stochastik9.png]] | ||
Version vom 5. Oktober 2008, 18:19 Uhr
- Von Philipp Issle übernommen!!!
- von: LK Mathematik 2008 10/Lösungen Stochastik Link-Text
- Mit dem Ziel der Verbesserung der Aufgabe 7
Zu Aufgabe 7
- In einer Urne befinden sich fünf von 1 bis 5 nummerierte Kugeln! Es werden
a) 2 Kugeln nacheinander ohne zurücklegen gezogen
- Möglicher Ergebnissraum wäre dann Ω = {12,13,14,15,23,24,25,34,35,45};
- Bei der ersten Kugel gib es 4 Möglichkeiten, bei der zweiten Kugel 3, bei der dritten Kugel 2 und bei der vierten Kugel 1 Möglichkeit.
- Mächtigkeit ist |Ω|= 4+3+2+1=10
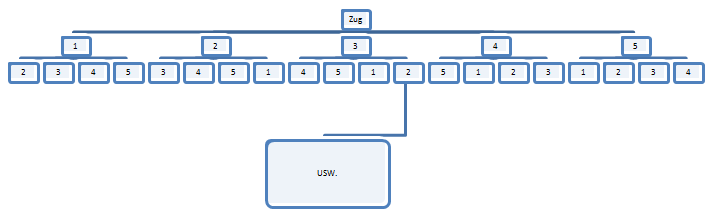
b) 3 Kugeln gleichzeitig gezogen
Splitten wir es mal auf und tuen so, als ob jede Kugel einzeln gezogen wird jedoch nicht mehr zurückgelegt wird. Dann gibt es am Anfang mit dem Zug der ersten Kugel 6 Möglichkeiten, bei der zweiten Kugel 3 Möglichkeiten und bei der dritten Kugel nur 1 Möglichkeit.
- Möglicher Ergebnissraum wäre dann Ω = {123,124,125,134,135,145,234,235,245,345}
- Mächtigkeit ist |Ω|= 6+3+1=10