Abi 2013 Analysis II Teil A: Unterschied zwischen den Versionen
M12KH3 (Diskussion | Beiträge) |
M12KH3 (Diskussion | Beiträge) |
||
| Zeile 78: | Zeile 78: | ||
;Aufgabe 4 | ;Aufgabe 4 | ||
| − | [[Bild:Abi2013 AII TeilA 4. | + | [[Bild:Abi2013 AII TeilA 4.pdf|center|350px]] |
Abbildung 1 zeigt den Graphen G<sub>f</sub> der Funktion f mit Definitionsbereich [-2;2]. Der Graph besteht aus zwei Halbkreisen, die die Mittelpunkte (-1/0) bzw. (1/0) sowie jeweils den Radius 1 besitzen. Betrachtet wird die in [-2;2] definierte Integralfunktion <math> F:x \mapsto \int_{0}^{x} f (t)\,dt </math>. | Abbildung 1 zeigt den Graphen G<sub>f</sub> der Funktion f mit Definitionsbereich [-2;2]. Der Graph besteht aus zwei Halbkreisen, die die Mittelpunkte (-1/0) bzw. (1/0) sowie jeweils den Radius 1 besitzen. Betrachtet wird die in [-2;2] definierte Integralfunktion <math> F:x \mapsto \int_{0}^{x} f (t)\,dt </math>. | ||
| Zeile 87: | Zeile 87: | ||
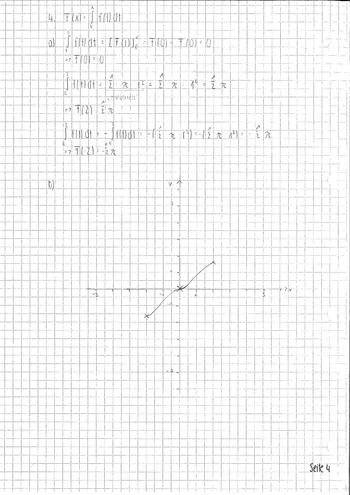
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild:ABI2013_AII_TeilA_4ab_Lös. | + | [[Bild:ABI2013_AII_TeilA_4ab_Lös.pdf|700px]] |
}} | }} | ||
Version vom 17. April 2018, 23:51 Uhr
|
|
Geben Sie für die Funktion f mit 
|
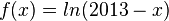den maximalen Definitionsbereich, das Verhalten von f an den Grenzen von D sowie die Schnittpunkte des Graphen von f mit den Koordinatenachsen an.
Der Graph der in IR definierten Funktion  |
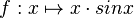verläuft durch den Koordinatenursprung. Berechnen Sie f(0) und geben Sie das Krümmungsverhalten des Graphen von f in unmittelbarer Nähe des Koordinatenursprungs an.
Gegeben sind die in IR definierten Funktionen  |
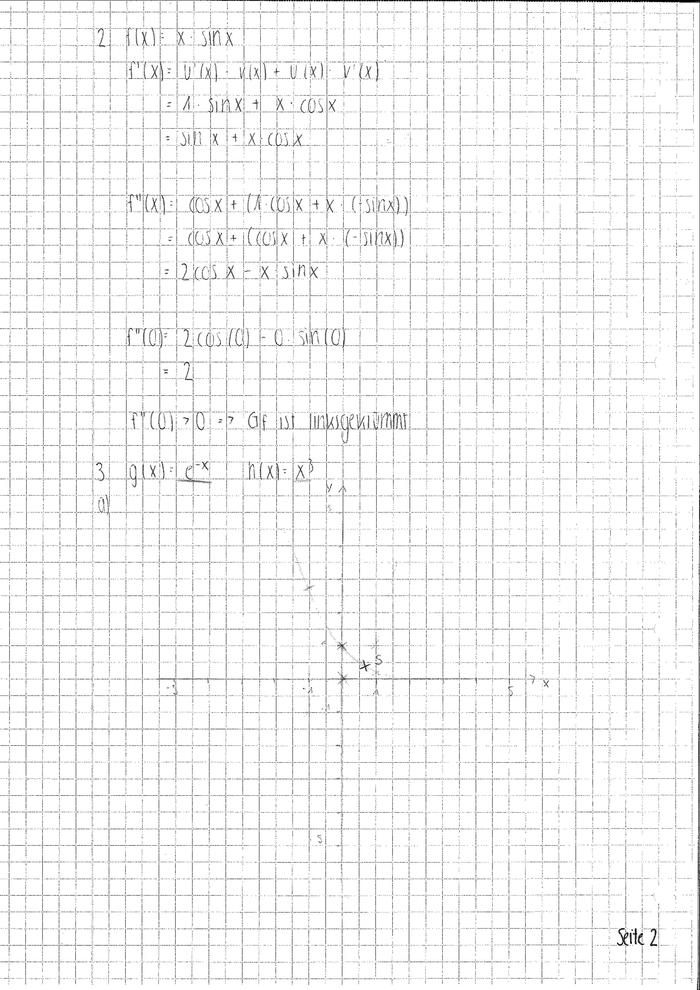
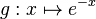und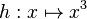 
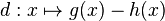den ersten Schritt des Newton-Verfahren mit dem Startwert x0=1 durchführen.
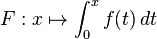 Abbildung 1 zeigt den Graphen Gf der Funktion f mit Definitionsbereich [-2;2]. Der Graph besteht aus zwei Halbkreisen, die die Mittelpunkte (-1/0) bzw. (1/0) sowie jeweils den Radius 1 besitzen. Betrachtet wird die in [-2;2] definierte Integralfunktion a) Geben Sie F(0), F(2) und F(-2) an. b) Skizzieren Sie den Graphen von F in Abbildung 1. |
.
