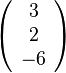Abi 2013 Geometrie I Teil B: Unterschied zwischen den Versionen
| Zeile 22: | Zeile 22: | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
| + | Ein auf einer horizontalen Fläche stehendes Kunstwerk besitzt einen Grundkörper aus massivem Beton, der die Form eines Spats hat. Alle Seitenflächen eines Spats sind Parallelogramme. | ||
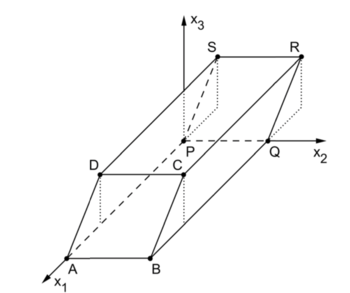
| + | In einem Modell lässt sich der Grundkörper durch einen Spat ABCDPQRS mit A(28|0|0), B(28|10|0), D(20|0|6) und P(0|0|0) beschreiben (vgl.Ab- | ||
| + | bildung). Die rechteckige Grundfläche ABQP liegt in der x<sub>1</sub>x<sub>2</sub> -Ebene. Im Koordinatensystem entspricht eine Längeneinheit 0,1 m, d. h. der Grundkörper ist 0,6 m hoch. | ||
| + | [[Bild:ABI2013_GI_TeilB_1.png|center|350px]] | ||
| + | |||
a) | a) | ||
| + | Geben Sie die Koordinaten des Punkts C an und zeigen Sie, dass die Seitenfläche ABCD ein Quadrat ist. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2013_GI_TeilB_1a_Lös.jpg|700px]] |
}} | }} | ||
b) | b) | ||
| + | Ermitteln Sie eine Gleichung der Ebene E, in der die Seitenfläche ABCD liegt, in Normalenorm. | ||
| + | :: (mögliches Ergebnis E: 3x<sub>1</sub>+4<sub>3</sub>-84=0) | ||
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2013_GI_TeilB_1b_Lös.jpg|700px]] |
}} | }} | ||
c) | c) | ||
| + | Berechnen Sie die Größe des Winkels, unter dem die Seitenfläche ABCD gegen die x<sub>1</sub>x<sub>2</sub> -Ebene geneigt ist. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2013_GI_TeilB_1c_Lös.jpg|700px]] |
}} | }} | ||
| + | d) | ||
| + | Die Seitenfläche PQRS liegt in einer Ebene F. Bestimmen Sie, ohne zu rechnen, eine Gleichung von F in Normalenform; erläutern Sie Ihr Vorgehen. | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:ABI2013_GI_TeilB_1d_Lös.jpg|700px]] | ||
| + | }} | ||
| − | + | e) | |
| + | Machen Sie plausibel, dass das Volumen des Spats mithilfe der Formel V = G⋅h berechnet werden kann, wobei G der Flächeninhalt des Recht- | ||
| + | ecks ABQP und h die zugehörige Höhe des Spats ist. | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:ABI2013_GI_TeilB_1e_Lös.jpg|700px]] | ||
| + | }} | ||
| + | f) | ||
| + | Ein Kubikmeter des verwendeten Betons besitzt eine Masse von 2,1 t. Berechnen Sie die Masse des Grundkörpers. | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:ABI2013_GI_TeilB_1f_Lös.jpg|700px]] | ||
| + | }} | ||
| + | Der Grundkörper ist mit einer dünnen geradlinigen Bohrung versehen, die im Modell vom Punkt H(11| 3 | 6) der Deckfläche DCRS aus in Richtung des Schnittpunkts der Diagonalen der Grundfläche verläuft. In der Bohrung ist eine gerade Stahlstange mit einer Länge von 1,4 m so befestigt, dass die Stange zu drei Vierteln ihrer Länge aus der Deckfläche herausragt. | ||
| + | |||
| + | g) | ||
| + | Bestimmen Sie im Modell eine Gleichung der Geraden h, entlang derer die Bohrung verläuft, sowie die Koordinaten des Punkts, in dem die Stange in der Bohrung endet. | ||
| + | :: (zur Kontrolle: möglicher Richtungsvektor von h: <math>\left( \begin{array}{c}3\\2\\-6\end{array} \right) </math> | ||
| + | |||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:ABI2013_GI_TeilB_1g_Lös.jpg|700px]] | ||
| + | }} | ||
| + | |||
| + | h) | ||
| + | Auf der Deckfläche des Grundkörpers liegt eine Stahlkugel mit einem Radius von 0,8 m. Im Modell berührt die Kugel die Deckfläche des Spats im Punkt K. Beschreiben Sie, wie man im Modell rechnerisch überprüfen könnte, ob die Stahlkugel die Stange berührt, wenn die Koordinaten von K bekannt wären. | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:ABI2013_GI_TeilB_1h_Lös.jpg|700px]] | ||
| + | }} | ||
| + | |||
| + | </td></tr></table></center> | ||
</div> | </div> | ||
Aktuelle Version vom 15. April 2018, 11:31 Uhr
|
|
Ein auf einer horizontalen Fläche stehendes Kunstwerk besitzt einen Grundkörper aus massivem Beton, der die Form eines Spats hat. Alle Seitenflächen eines Spats sind Parallelogramme. In einem Modell lässt sich der Grundkörper durch einen Spat ABCDPQRS mit A(28|0|0), B(28|10|0), D(20|0|6) und P(0|0|0) beschreiben (vgl.Ab- bildung). Die rechteckige Grundfläche ABQP liegt in der x1x2 -Ebene. Im Koordinatensystem entspricht eine Längeneinheit 0,1 m, d. h. der Grundkörper ist 0,6 m hoch. a) Geben Sie die Koordinaten des Punkts C an und zeigen Sie, dass die Seitenfläche ABCD ein Quadrat ist. b) Ermitteln Sie eine Gleichung der Ebene E, in der die Seitenfläche ABCD liegt, in Normalenorm.
c) Berechnen Sie die Größe des Winkels, unter dem die Seitenfläche ABCD gegen die x1x2 -Ebene geneigt ist. d) Die Seitenfläche PQRS liegt in einer Ebene F. Bestimmen Sie, ohne zu rechnen, eine Gleichung von F in Normalenform; erläutern Sie Ihr Vorgehen. e) Machen Sie plausibel, dass das Volumen des Spats mithilfe der Formel V = G⋅h berechnet werden kann, wobei G der Flächeninhalt des Recht- ecks ABQP und h die zugehörige Höhe des Spats ist. f) Ein Kubikmeter des verwendeten Betons besitzt eine Masse von 2,1 t. Berechnen Sie die Masse des Grundkörpers. Der Grundkörper ist mit einer dünnen geradlinigen Bohrung versehen, die im Modell vom Punkt H(11| 3 | 6) der Deckfläche DCRS aus in Richtung des Schnittpunkts der Diagonalen der Grundfläche verläuft. In der Bohrung ist eine gerade Stahlstange mit einer Länge von 1,4 m so befestigt, dass die Stange zu drei Vierteln ihrer Länge aus der Deckfläche herausragt. g) Bestimmen Sie im Modell eine Gleichung der Geraden h, entlang derer die Bohrung verläuft, sowie die Koordinaten des Punkts, in dem die Stange in der Bohrung endet.
h) Auf der Deckfläche des Grundkörpers liegt eine Stahlkugel mit einem Radius von 0,8 m. Im Modell berührt die Kugel die Deckfläche des Spats im Punkt K. Beschreiben Sie, wie man im Modell rechnerisch überprüfen könnte, ob die Stahlkugel die Stange berührt, wenn die Koordinaten von K bekannt wären. |