Bentutzer:Gebauer David/Lk Mathematik: Unterschied zwischen den Versionen
Aus RMG-Wiki
(Die Seite wurde neu angelegt: == Hausaufgabe zur Integralen Flächenberechnung zweier sich schneidenden Funktionen ==) |
(→Hausaufgabe zur Integralen Flächenberechnung zweier sich schneidenden Funktionen) |
||
| Zeile 1: | Zeile 1: | ||
== Hausaufgabe zur Integralen Flächenberechnung zweier sich schneidenden Funktionen == | == Hausaufgabe zur Integralen Flächenberechnung zweier sich schneidenden Funktionen == | ||
| + | |||
| + | |||
| + | '''Aufgabe:''' <br> | ||
| + | Es soll der Inhalt des Segments, das die Gerade mit der Gleichung y-4=0 vom Graphen der Funktion <math>f: x\rightarrow \frac{1}{2} x^2</math> abschneidet, berechnet werden! | ||
| + | '''Lösung''' <br> | ||
| + | <math>A= \int_{-4}^{4} f (4-\frac{1}{4} x^2)\,dx =</math><math>\left[ 4x - \frac{1}{4}*\frac{x^3}{3}\right]^4_{-4} </math> =... <math>\frac{64}{3}</math> | ||
Aktuelle Version vom 24. September 2008, 09:23 Uhr
Hausaufgabe zur Integralen Flächenberechnung zweier sich schneidenden Funktionen
Aufgabe:
Es soll der Inhalt des Segments, das die Gerade mit der Gleichung y-4=0 vom Graphen der Funktion 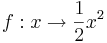 abschneidet, berechnet werden!
Lösung
abschneidet, berechnet werden!
Lösung
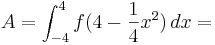
![\left[ 4x - \frac{1}{4}*\frac{x^3}{3}\right]^4_{-4}](/images/math/f/7/e/f7ecb2a050627ecb2136a5188b0bc1ea.png) =...
=...