Abi 2016 Stochastik I Teil A: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 26: | Zeile 26: | ||
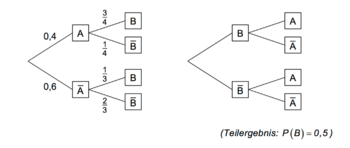
| − | Die beiden Baumdiagramme gehören zum selben Zufallsexperiment mit den | + | Die beiden Baumdiagramme gehören zum selben Zufallsexperiment mit den Ereignissen A und B. Berechnen Sie die Wahrscheinlichkeit P(B) und ergänzen Sie anschließend |
| − | Ereignissen A und B. | + | an allen Ästen des rechten Baumdiagramms die zugehörigen Wahrscheinlichkeiten. |
| − | Berechnen Sie die Wahrscheinlichkeit P(B) und ergänzen Sie anschließend | + | [[Bild:ABI2016_SI_TeilA_1.png|center|350px]] |
| − | an allen Ästen des rechten Baumdiagramms die zugehörigen | + | |
| − | + | ||
| − | [[Bild:ABI2016_SI_TeilA_1. | + | |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
Aktuelle Version vom 28. März 2018, 14:45 Uhr
|
|
|
Bei einem Zufallsexperiment wird eine ideale Münze so lange geworfen, bis zum zweiten Mal Zahl (Z) oder zum zweiten Mal Wappen (W) oben liegt. Als Ergebnismenge wird festgelegt: {ZZ; WW; ZWZ; ZWW; WZZ; WZW}. a) Begründen Sie, dass dieses Zufallsexperiment kein Laplace-Experiment ist. b) Die Zufallsgröße X ordnet jedem Ergebnis die Anzahl der entsprechenden Münzwürfe zu. Berechnen Sie den Erwartungswert von X.
|