Abi 2016 Analysis II Teil B: Unterschied zwischen den Versionen
| Zeile 67: | Zeile 67: | ||
;Aufgabe 2 | ;Aufgabe 2 | ||
| − | a) | + | Eine zweite Modellierung des Querschnitts der Tunnelwand verwendet eine Kosinusfunktion vom Typ k : x→5⋅cos(c⋅x), mit c ∈ IR und Definitionsbereich D<sub>k</sub>=[-5;5], bei der offensichtlich Bedingung II erfüllt ist.<br /> |
| + | |||
| + | |||
| + | a) Bestimmen Sie c so, dass auch Bedingung I erfüllt ist, und berechnen Sie damit den Inhalt der Querschnittsfläche des Tunnels.<br /> | ||
| + | (zur Kontrolle: <math>c=\frac{\pi}{10}</math> Inhalt der Querschnittfläche: <math>c=\frac{100}{\pi}m^{2}</math>) | ||
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2016_AII_TeilB_2a_Lös.jpg|700px]] | [[Bild:ABI2016_AII_TeilB_2a_Lös.jpg|700px]] | ||
}} | }} | ||
| − | b) | + | b)Zeigen Sie, dass Bedingung III weder bei einer Modellierung mit p aus Aufgabe 1 noch bei einer Modellierung mit k erfüllt ist. |
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2016_AII_TeilB_2b_Lös.jpg|700px]] | [[Bild:ABI2016_AII_TeilB_2b_Lös.jpg|700px]] | ||
| Zeile 90: | Zeile 96: | ||
;Aufgabe 3 | ;Aufgabe 3 | ||
| − | a) | + | Eine dritte Modellierung des Querschnitts der Tunnelwand, bei der ebenfalls die Bedingungen I und II erfüllt sind, verwendet die Funktion <math>f:x\mapsto \sqrt{25-x^{2}}</math> mit Definitionsbereich D<sub>f</sub>=[-5;5].<br /> |
| + | |||
| + | a)Begründen Sie, dass in diesem Modell jeder Punkt des Querschnitts der Tunnelwand von der Bodenmitte M den Abstand 5 m hat. | ||
| + | Zeichnen Sie den Graphen von f in ein Koordinatensystem ein (Platzbedarf im Hinblick auf spätere Aufgaben: -5 ≤ x ≤ 9 ; -1 ≤ y ≤ 13) undbe- gründen Sie, dass bei dieser Modellierung auch Bedingung III erfüllt ist. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
Version vom 27. März 2018, 22:03 Uhr
|
|
Im Rahmen eines W-Seminars modellieren Schülerinnen und Schüler einen Tunnelquerschnitt, der senkrecht zum Tunnelverlauf liegt. Dazu beschreiben sie den Querschnitt der Tunnelwand durch den Graphen einer Funktion in einem Koordinatensystem. Der Querschnitt des Tunnelbodens liegt dabei auf der x-Achse, sein Mittelpunkt M im Ursprung des Koordinatensystems; eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität. Für den Tunnelquerschnitt sollen folgende Bedingungen gelten: I Breite des Tunnelbodens: b=10m II Höhe des Tunnels an der höchsten Stelle: h=5m III Der Tunnel ist auf einer Breite von mindestens 6m mindestens 4m hoch.
Die Schülerinnen und Schüler untersuchen nun den Abstand d(x) der Graphenpunkte Px(x/p(x)) vom Ursprung des Koordinatensystems. b) Zeigen Sie, dass c) Es gibt Punkte des Querschnitts der Tunnelwand, deren Abstand zu M minimal ist. Bestimmen Sie die x-Koordinaten der Punkte Px , für die d(x) minimal ist, und geben Sie davon ausgehend diesen minimalen Abstand an.
|
Eine zweite Modellierung des Querschnitts der Tunnelwand verwendet eine Kosinusfunktion vom Typ k : x→5⋅cos(c⋅x), mit c ∈ IR und Definitionsbereich Dk=[-5;5], bei der offensichtlich Bedingung II erfüllt ist.
b)Zeigen Sie, dass Bedingung III weder bei einer Modellierung mit p aus Aufgabe 1 noch bei einer Modellierung mit k erfüllt ist.
|
Eine dritte Modellierung des Querschnitts der Tunnelwand, bei der ebenfalls die Bedingungen I und II erfüllt sind, verwendet die Funktion a)Begründen Sie, dass in diesem Modell jeder Punkt des Querschnitts der Tunnelwand von der Bodenmitte M den Abstand 5 m hat. Zeichnen Sie den Graphen von f in ein Koordinatensystem ein (Platzbedarf im Hinblick auf spätere Aufgaben: -5 ≤ x ≤ 9 ; -1 ≤ y ≤ 13) undbe- gründen Sie, dass bei dieser Modellierung auch Bedingung III erfüllt ist. b) c) d) e)
|
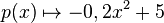 mit Definitionsbereich
mit Definitionsbereich  = [-5, 5]
= [-5, 5]
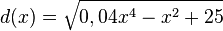 gilt.
gilt.
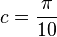 Inhalt der Querschnittfläche:
Inhalt der Querschnittfläche: 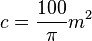 )
)
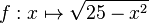 mit Definitionsbereich Df=[-5;5].
mit Definitionsbereich Df=[-5;5].
