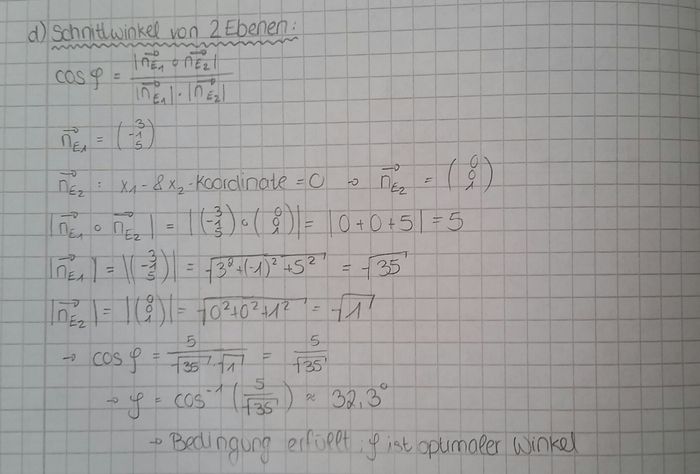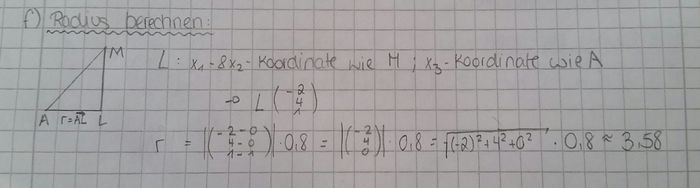Abi 2017 Geometrie I Teil B: Unterschied zwischen den Versionen
Aus RMG-Wiki
(Die Seite wurde neu angelegt: „__NOTOC__ <div style="padding:1px;background: #EEEEE6;border:0px groove;"> <center><table border="0" width="800px" cellpadding=5 cellspacing=15> <tr><td wid…“) |
|||
| Zeile 20: | Zeile 20: | ||
<center><table border="0" width="800px" cellpadding=5 cellspacing=15> | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | In einem kartesischen Koordinatensystem sind die Punkte A (0|0|1), | ||
| + | B (2|6|1), C (-4|8|5) und D (-6|2|5) gegeben. Sie liegen in einer | ||
| + | Ebene E und bilden ein Viereck ABCD, dessen Diagonalen sich im | ||
| + | Punkt M schneiden. | ||
| + | |||
| − | a) | + | a) Begründen Sie, dass die Gerade AB parallel zur x<sub>1</sub>x<sub>2</sub>-Ebene verläuft. |
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 27: | Zeile 34: | ||
}} | }} | ||
| − | b) | + | b) Weisen Sie nach, dass das Viereck ABCD ein Rechteck ist. Bestimmen |
| + | Sie die Koordinaten von M. | ||
| + | (Teilergebnis: M (-2|4|3) | ||
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 33: | Zeile 43: | ||
}} | }} | ||
| − | c) | + | c) Ermitteln Sie eine Gleichung der Ebene E in Normalenform. |
| + | (mögliches Ergebnis: E: 3x<sub>1</sub>-x<sub>2</sub>+5x<sub>3</sub>-5=0) | ||
| + | |||
| + | |||
[[Bild:ABI2017_GII_TeilB_1c.jpg|right|350px]] | [[Bild:ABI2017_GII_TeilB_1c.jpg|right|350px]] | ||
Version vom 26. Juli 2017, 08:30 Uhr
|
|
|
In einem kartesischen Koordinatensystem sind die Punkte A (0|0|1), B (2|6|1), C (-4|8|5) und D (-6|2|5) gegeben. Sie liegen in einer Ebene E und bilden ein Viereck ABCD, dessen Diagonalen sich im Punkt M schneiden.
b) Weisen Sie nach, dass das Viereck ABCD ein Rechteck ist. Bestimmen Sie die Koordinaten von M. (Teilergebnis: M (-2|4|3)
c) Ermitteln Sie eine Gleichung der Ebene E in Normalenform. (mögliches Ergebnis: E: 3x1-x2+5x3-5=0)
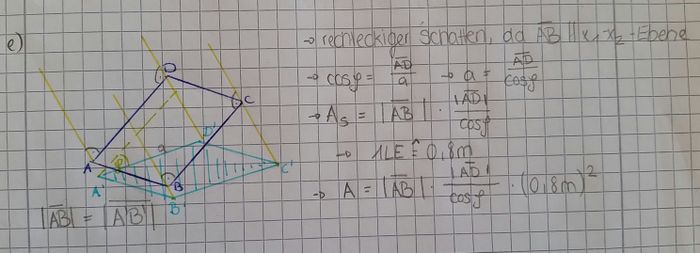
d) e) f) |