Abi 2013 Analysis II Teil A: Unterschied zwischen den Versionen
| Zeile 59: | Zeile 59: | ||
;Aufgabe 3 | ;Aufgabe 3 | ||
| − | + | Gegeben sind die in IR definierten Funktionen <math> g:x \mapsto e^{-x} </math> und <math> h: x \mapsto x^3 </math> <br> | |
| − | a) Veranschaulichen Sie durch eine Skizze, dass die Graphen von g und h | + | a) Veranschaulichen Sie durch eine Skizze, dass die Graphen von g und h genau einen Schnittpunkt haben. <br> |
| − | genau einen Schnittpunkt haben. | + | b) Bestimmen Sie einen Näherungswert x<sub>1</sub> für die x-Koordinate dieses Schnittpunkts, indem Sie für die in IR definierte Funktion |
| − | b) Bestimmen Sie einen Näherungswert | + | <math> d: x \mapsto g(x)-h(x)</math> den ersten Schritt des Newton-Verfahren mit dem Startwert x=1 durchführen. |
| − | d: x | + | |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
Version vom 20. Juli 2017, 16:44 Uhr
|
|
Geben Sie für die Funktion f mit
|
Der Graph der in IR definierten Funktion |
Gegeben sind die in IR definierten Funktionen |
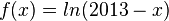 den maximalen Definitionsbereich, das Verhalten von f an den Grenzen von D sowie die Schnittpunkte des Graphen von f mit den Koordinatenachsen an.
den maximalen Definitionsbereich, das Verhalten von f an den Grenzen von D sowie die Schnittpunkte des Graphen von f mit den Koordinatenachsen an.
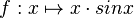 verläuft durch den Koordinatenursprung. Berechnen Sie f(0) und geben Sie das Krümmungsverhalten des Graphen von f in unmittelbarer Nähe des Koordinatenursprungs an.
verläuft durch den Koordinatenursprung. Berechnen Sie f(0) und geben Sie das Krümmungsverhalten des Graphen von f in unmittelbarer Nähe des Koordinatenursprungs an.
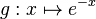 und
und