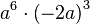BMT 10 2016: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
Zeile 6: Zeile 6:
 
<center><span style="background:yellow">Falls es Probleme mit der Ansicht gibt, bitte [[Firefox]] als [[Browser]] verwenden!</span></center>
 
<center><span style="background:yellow">Falls es Probleme mit der Ansicht gibt, bitte [[Firefox]] als [[Browser]] verwenden!</span></center>
  
−
=Aufgabe 1=
 
  
−
{{Kurzinfo-2|DSB ISB|DSB-1}}
 
 
<div style="padding:10px;background:#ffffff;border:1px groove;">
 
<div style="padding:10px;background:#ffffff;border:1px groove;">
 
<big>'''Aufgabe 1'''</big>
 
<big>'''Aufgabe 1'''</big>
Zeile 26: Zeile 24:
 
</div>
 
</div>
  
−
===Aufgabe 2===
 
  
 
<div style="padding:10px;background:#ffffff;border:1px groove;">
 
<div style="padding:10px;background:#ffffff;border:1px groove;">
 
<big>'''Aufgabe 2'''</big>
 
<big>'''Aufgabe 2'''</big>
−
 
+
[[Datei:BMT 10 2016 A2.jpg|220px|right]]
 
Sophie hat mithilfe einer Schnur den Um-
 
Sophie hat mithilfe einer Schnur den Um-
 
fang U des abgebildeten Baumstamms  
 
fang U des abgebildeten Baumstamms  
Zeile 63: Zeile 60:
 
|style="vertical-align:top"|'''c)'''
 
|style="vertical-align:top"|'''c)'''
 
|width="5px"|
 
|width="5px"|
−
|Mit der Gleichung der Form III und dem passenden Wert für a berechnet Simon den y-Wert für x = 6. Beschreiben Sie die Bedeutung dieses y-Werts im Sachzusammenhang.
+
|Eine 120-jährige Buche hat einen Stamm mit einer Trockenmasse von 1,9 t. Für den Aufbau ihres Stamms hat sie der Atmosphäre im Laufe ihres bisherigen Lebens 3,5 t  CO<sub>2</sub> entnommen. Wie viele kg CO<sub>2</sub>  sind dies durchschnittlich pro Jahr? Kreuzen Sie nur den richtigen Term an.
 +
 
 +
...Terme fehlen noch ... Bild hochladen oder multiple Choice einfügen
 +
 
 
|}
 
|}
  
 
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 
:{{Lösung versteckt|1=
 
:{{Lösung versteckt|1=
−
:Der y-Wert steht für die Höhe der Brücke in 6m Entfernung vom linken Auflagepunkt (bzw. in 2m Entfernung vom rechten Auflagepunkt).
+
:
 
}}
 
}}
 
</div>
 
</div>
Zeile 76: Zeile 76:
 
<div style="padding:10px;background:#ffffff;border:1px groove;">
 
<div style="padding:10px;background:#ffffff;border:1px groove;">
 
<big>'''Aufgabe 3'''</big>
 
<big>'''Aufgabe 3'''</big>
 +
[[Datei:BMT 10 2016 A3.jpg|220px|right]]
 +
xyz
 +
{|
 +
|style="vertical-align:top"|'''a)'''
 +
|width="5px"|
 +
|xyz
 +
|}
 +
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 +
:{{Lösung versteckt|1=
 +
:
 +
}}
 +
</div>
  
−
Ein Laplace-Würfel, der mit den Zahlen 1 bis 6 beschriftet ist, wird zweimal nacheinander geworfen. Bestimmen Sie die Wahrscheinlichkeit dafür, dass man die Augensumme 10 erhält.
+
{|
 +
|style="vertical-align:top"|'''b)'''
 +
|width="5px"|
 +
|xyz
 +
|}
 +
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 +
:{{Lösung versteckt|1=
 +
:
 +
}}
 +
</div>
  
 +
{|
 +
|style="vertical-align:top"|'''c)'''
 +
|width="5px"|
 +
|xyz
 +
|}
 
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 
:{{Lösung versteckt|1=
 
:{{Lösung versteckt|1=
−
:P("Die Augensumme ist 10") = P(46; 55; 64)= <math>\frac{1}{6}\cdot\frac{1}{6}\cdot 3</math> = <math>\frac{1}{12}</math>
+
:
 
}}
 
}}
 +
</div>
 
</div>
 
</div>
 
</div>
 
</div>
Zeile 89: Zeile 116:
 
<div style="padding:10px;background:#ffffff;border:1px groove;">
 
<div style="padding:10px;background:#ffffff;border:1px groove;">
 
<big>'''Aufgabe 4'''</big>
 
<big>'''Aufgabe 4'''</big>
−
[[file:BMT 10 2011 A4.jpg|220px|right]]
+
[[Datei:BMT 10 2016 A4.jpg|220px|right]]
−
Die Abbildung zeigt eine Pyramide der Höhe h. Die quadratische Grundfläche hat die Seitenlänge a, jedes Seitendreieck die Höhe m.
+
xyz
−
 
+
−
 
+
−
 
+
 
{|
 
{|
 
|style="vertical-align:top"|'''a)'''
 
|style="vertical-align:top"|'''a)'''
 
|width="5px"|
 
|width="5px"|
−
|Ergänzen Sie die Gleichung
+
|xyz
−
 
+
−
::h = ______
+
−
 
+
−
durch einen Term, mit dem h aus a und m berechnet werden kann.
+
 
|}
 
|}
−
 
−
 
 
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 
:{{Lösung versteckt|1=
 
:{{Lösung versteckt|1=
−
:m ist die Hypotenuse, h und <math>\frac{a}{2}</math> sind die Katheten eines rechtwinkligen Dreiecks. Es gilt der Satz des Pythagoras.
+
:
−
 
+
−
:<math>(\frac{a}{2})^2 + h^2 = m^2</math> 
+
−
 
+
−
:''Auflösen nach h ergibt:''
+
−
 
+
−
:<math>h = \sqrt{m^2 - (\frac{a}{2})^2} </math>
+
 
}}
 
}}
−
</div>
 
 
</div>
 
</div>
  
 
{|
 
{|
−
|<div class="multiplechoice-quiz">
+
|style="vertical-align:top"|'''b)'''
−
<big>'''Aufgabe 4b'''</big>
+
|width="5px"|
−
 
+
|xyz
−
Mit welchen der folgenden Gleichungen lässt sich der Neigungswinkel <math>\varphi</math> einer Seitenfläche gegen die Grundfläche berechnen? Kreuzen Sie an.
+
|}
−
 
+
<div style="padding:1px;background:#ddeeff;border:1px groove;">
−
(<math>tan\varphi = \frac{2h}{a}</math>)
+
:{{Lösung versteckt|1=
−
(!<math>tan\varphi = \frac{a}{2h}</math>)
+
:
−
(!<math>sin\varphi = \frac{a}{2m}</math>)
+
}}
−
(<math>sin\varphi = \frac{h}{m}</math>)
+
−
(!<math>sin\varphi = \frac{m}{2h}</math>)
+
−
 
+
 
</div>
 
</div>
 +
 +
{|
 +
|style="vertical-align:top"|'''c)'''
 +
|width="5px"|
 +
|xyz
 
|}
 
|}
 +
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 +
:{{Lösung versteckt|1=
 +
:
 +
}}
 +
</div>
 +
</div>
 +
</div>
  
  
Zeile 138: Zeile 158:
 
<big>'''Aufgabe 5'''</big>
 
<big>'''Aufgabe 5'''</big>
  
−
Auf einem Spielfeld, das 100 m lang und 75 m breit ist, findet ein Fußballspiel statt. Ein Spieler
+
{|
−
passt den Ball zu einem Mitspieler; dabei ist der Ball zwei Sekunden unterwegs. Schätzen Sie den Anteil der Spielfeldfläche ab, den die zehn Feldspieler der gegnerischen Mannschaft in dieser Zeit höchstens abdecken können. Gehen Sie dazu davon aus, dass die Durchschnittsgeschwindigkeit der Spieler, während der Ball unterwegs ist, 5 <math>\frac{m}{s}</math> beträgt. Erläutern Sie Ihr Vorgehen.
+
|style="vertical-align:top"|'''a)'''
−
 
+
|width="5px"|
 +
|xyz
 +
|}
 
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 
:{{Lösung versteckt|1=
 
:{{Lösung versteckt|1=
−
:Weg pro Spieler in 2 Sekunden: 5<math>\frac{m}{s}</math> · 2s = 10m
+
:
 +
}}
 +
</div>
  
−
:höchstens abgedeckte Fläche pro Feldpieler (Kreis mit Radius 10m): (10m)<sup>2</sup><math>\pi</math> = 100<math>\pi</math> m<sup>2</sup>
+
{|
−
 
+
|style="vertical-align:top"|'''b)'''
−
:von zehn Feldspielern höchstens abgedeckte Fläche: 1000<math>\pi</math> m<sup>2</sup>
+
|width="5px"|
−
 
+
|xyz
−
:Spielfeldfläche: 100m · 75m = 7500m<sup>2</sup>  
+
|}
−
 
+
<div style="padding:1px;background:#ddeeff;border:1px groove;">
−
:Anteil der Spielfeldfläche, die von zehn Feldspielern in 2 Sekunden höchstens abgedeckt werden kann:
+
:{{Lösung versteckt|1=
−
 
+
:
−
:<math>\frac{1000\pi m^2}{7000 m^2} \approx \frac{3000}{7500} = \frac {2}{5} = 40% </math>
+
 
}}
 
}}
 
</div>
 
</div>
Zeile 161: Zeile 184:
 
<div style="padding:10px;background:#ffffff;border:1px groove;">
 
<div style="padding:10px;background:#ffffff;border:1px groove;">
 
<big>'''Aufgabe 6'''</big>
 
<big>'''Aufgabe 6'''</big>
−
 
−
Bestimmen Sie die Lösung folgender Gleichung (<math>x \in \mathbb{R} \backslash \lbrace{0;\frac{5}{4}\rbrace</math>).
 
−
 
−
:<math>\frac{1}{4x-5}-\frac{1}{6x}=0</math>
 
  
  
 
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 
:{{Lösung versteckt|1=
 
:{{Lösung versteckt|1=
−
:<math>\frac{1}{4x-5}-\frac{1}{6x}=0</math> 
+
 
−
:6x - (4x - 5) = 0 
+
−
:6x - 4x + 5 = 0 
+
−
:2x + 5 = 0 
+
−
:x = -2,5
+
 
}}
 
}}
 
</div>
 
</div>
Zeile 182: Zeile 197:
 
<big>'''Aufgabe 7'''</big>
 
<big>'''Aufgabe 7'''</big>
 
{|
 
{|
−
|Im Dreieck ABC sind M<sub>a</sub> , M<sub>b</sub> und M<sub>c</sub> die Mittelpunkte der Seiten (vgl. Abbildung). Die Verbindungsstrecken dieser Mittelpunkte mit den gegenüberliegenden Eckpunkten schneiden sich im Punkt S.
+
|
−
|[[Datei:BMT 10 2011 A7.jpg|220px|right]]
+
|[[Datei:BMT 10 2016 A7.jpg|220px|right]]
 
|}
 
|}
 
{|
 
{|
 
|style="vertical-align:top"|'''a)'''
 
|style="vertical-align:top"|'''a)'''
 
|width="5px"|
 
|width="5px"|
−
|Die Dreiecke AM<sub>c</sub>S und M<sub>c</sub>BS haben den gleichen Flächeninhalt, da sie in der Länge einer Seite und der zugehörigen Höhe übereinstimmen. Tragen Sie diese Strecken deutlich sichtbar in die Abbildung ein.
+
|
 
|}
 
|}
 
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 
:{{Lösung versteckt|1=
 
:{{Lösung versteckt|1=
−
:[[Datei:BMT 10 2011 A7a.jpg|300px]]
+
:
 
}}
 
}}
 
</div>
 
</div>
Zeile 200: Zeile 215:
 
|style="vertical-align:top"|'''b)'''
 
|style="vertical-align:top"|'''b)'''
 
|width="5px"|
 
|width="5px"|
−
|Analog zu Aufgabe 7a kann man zeigen, dass zwei weitere Paare von Dreiecken mit gemeinsamem Eckpunkt S jeweils den gleichen Flächeninhalt haben. Die übereinstimmenden Inhalte sind mit X, Y und Z bezeichnet (vgl. Abbildung).
+
|
−
 
+
−
Begründen Sie, dass die Aussagen 2Z + X = 2Y + X sowie 2Z + Y = 2X + Y wahr sind,und folgern Sie daraus, dass X = Y = Z gilt.
+
 
|}
 
|}
 
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 
<div style="padding:1px;background:#ddeeff;border:1px groove;">
 
:{{Lösung versteckt|1=
 
:{{Lösung versteckt|1=
−
:Die Dreiecke AM<sub>c</sub>C und M<sub>c</sub>BC sind inhaltsgleich, da sie in der Länge einer Seite und der dazugehörigen Höhe übereinstimmen. Es gilt daher: 2Z + X = 2Y + X
+
:
−
 
+
−
:Die Dreiecke AM<sub>a</sub>C und ABM<sub>a</sub> sind inhaltsgleich, da sie in der Länge einer Seite und der dazugehörigen Höhe übereinstimmen. Es gilt daher: 2Z + Y = 2X + Y
+
−
 
+
−
:Aus 2Z + X = 2Y + X folgt Z = Y, aus 2Z + Y = 2X + Y folgt Z = X. Es gilt also: X = Y = Z.
+
 
}}
 
}}
 
</div>
 
</div>
 
</div>
 
</div>

Version vom 11. Juli 2017, 03:54 Uhr

Test und Lösungshinweise zum Download
Falls es Probleme mit der Ansicht gibt, bitte Firefox als Browser verwenden!


Aufgabe 1

Vereinfachen Sie so weit wie möglich.

a^6\cdot\left(-2a\right)^3

xyz



Aufgabe 2

220px

Sophie hat mithilfe einer Schnur den Um- fang U des abgebildeten Baumstamms bestimmt und daraus den zugehörigen Ra- dius r berechnet. Sie hat r = 0,5 m erhalten.

a) Geben Sie einen Term an, mit dem man r aus U berechnen kann.


b) Schätzen Sie ab, welches Volumen der Teil des Baumstamms hat, der in der Abbildung zu sehen ist.


c) Eine 120-jährige Buche hat einen Stamm mit einer Trockenmasse von 1,9 t. Für den Aufbau ihres Stamms hat sie der Atmosphäre im Laufe ihres bisherigen Lebens 3,5 t CO2 entnommen. Wie viele kg CO2 sind dies durchschnittlich pro Jahr? Kreuzen Sie nur den richtigen Term an.

...Terme fehlen noch ... Bild hochladen oder multiple Choice einfügen


Aufgabe 3

220px

xyz

a) xyz
b) xyz
c) xyz

</div>


Aufgabe 4

220px

xyz

a) xyz
b) xyz
c) xyz

</div>


Aufgabe 5

a) xyz
b) xyz


Aufgabe 6



Aufgabe 7

220px
a)


b)
Von „http://rmg.zum.de/index.php?title=BMT_10_2016&oldid=69490“