Abi 2014 Analysis II Teil A: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „__NOTOC__ <div style="padding:1px;background: #EEEEE6;border:0px groove;"> <center><table border="0" width="800px" cellpadding=5 cellspacing=15> <tr><td wid…“) |
|||
| Zeile 23: | Zeile 23: | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
Geben Sie jeweils den Term einer in IR definierten periodischen Funktion an,die die angegebene Eigenschaft hat. | Geben Sie jeweils den Term einer in IR definierten periodischen Funktion an,die die angegebene Eigenschaft hat. | ||
| − | + | ||
| − | + | a) Der Graph der Funktion g geht aus dem Graphen der in IR definierten Funktion <math>x \mapsto sinx</math> durch Spiegelung an der y-Achse hervor. | |
| − | + | ||
| + | b) Die Funktion h hat den Wertebereich [1;3]. | ||
| + | |||
| + | c) Die Funktion k besitzt die Periode π. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 44: | Zeile 47: | ||
;Aufgabe 2 | ;Aufgabe 2 | ||
| + | Gegeben ist die in IR definierte Funktion f mit <math>f(x) = e^x \cdot (2x + x^2)</math>. | ||
| + | a) Bestimmen Sie die Nullstellen der Funktion f. | ||
| + | |||
| + | b) Zeigen Sie, dass die in IR definierte Funktion F mit <math>F(x) = x^2 \cdot e^x</math> eine Stammfunktion von f ist. Geben Sie eine Gleichung einer weiteren Stammfunktion G von f an, für die <math>G(1) = 2e</math> gilt. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 62: | Zeile 69: | ||
;Aufgabe 3 | ;Aufgabe 3 | ||
| + | Der Graph einer in IR definierten Funktion <math>g : x \mapsto g(x)</math> besitzt für -5 ≤ x ≤ 5 zwei Wendepunkte. Entscheiden Sie, welcher der Graphen I, II und III zur zweiten Ableitungsfunktion g´´ von g gehört. Begründen Sie Ihre Entscheidung. | ||
| + | '''"Graphen 1,2 und 3 einfuegen!"''' | ||
| Zeile 79: | Zeile 88: | ||
;Aufgabe 4 | ;Aufgabe 4 | ||
| + | '''"Graph einfuegen!"''' | ||
| + | |||
| + | In einem Koordinatensystem (vgl. Abbildung 1) werden alle Rechtecke betrachtet, die folgende Bedingungen erfüllen: | ||
| + | |||
| + | - Zwei Seiten liegen auf den Koordinatenachsen. | ||
| + | |||
| + | - Ein Eckpunkt liegt auf dem Graphen G<sub>f</sub> der Funktion <math>f : x \mapsto -lnx</math> mit 0 < x < 1. | ||
| + | |||
| + | Abbildung 1 zeigt ein solches Rechteck. | ||
| + | |||
| + | Unter den betrachteten Rechtecken gibt es eines mit größtem Flächeninhalt. | ||
| + | Berechnen Sie die Seitenlängen dieses Rechtecks. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
Version vom 7. Juli 2017, 15:03 Uhr
|
|
Geben Sie jeweils den Term einer in IR definierten periodischen Funktion an,die die angegebene Eigenschaft hat. a) Der Graph der Funktion g geht aus dem Graphen der in IR definierten Funktion b) Die Funktion h hat den Wertebereich [1;3]. c) Die Funktion k besitzt die Periode π.
|
Gegeben ist die in IR definierte Funktion f mit a) Bestimmen Sie die Nullstellen der Funktion f. b) Zeigen Sie, dass die in IR definierte Funktion F mit |
Der Graph einer in IR definierten Funktion
|
"Graph einfuegen!" In einem Koordinatensystem (vgl. Abbildung 1) werden alle Rechtecke betrachtet, die folgende Bedingungen erfüllen: - Zwei Seiten liegen auf den Koordinatenachsen. - Ein Eckpunkt liegt auf dem Graphen Gf der Funktion Abbildung 1 zeigt ein solches Rechteck. Unter den betrachteten Rechtecken gibt es eines mit größtem Flächeninhalt. Berechnen Sie die Seitenlängen dieses Rechtecks. |
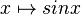 durch Spiegelung an der y-Achse hervor.
durch Spiegelung an der y-Achse hervor.
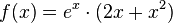 .
.
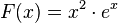 eine Stammfunktion von f ist. Geben Sie eine Gleichung einer weiteren Stammfunktion G von f an, für die
eine Stammfunktion von f ist. Geben Sie eine Gleichung einer weiteren Stammfunktion G von f an, für die 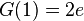 gilt.
gilt.
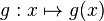 besitzt für -5 ≤ x ≤ 5 zwei Wendepunkte. Entscheiden Sie, welcher der Graphen I, II und III zur zweiten Ableitungsfunktion g´´ von g gehört. Begründen Sie Ihre Entscheidung.
"Graphen 1,2 und 3 einfuegen!"
besitzt für -5 ≤ x ≤ 5 zwei Wendepunkte. Entscheiden Sie, welcher der Graphen I, II und III zur zweiten Ableitungsfunktion g´´ von g gehört. Begründen Sie Ihre Entscheidung.
"Graphen 1,2 und 3 einfuegen!"
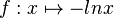 mit 0 < x < 1.
mit 0 < x < 1.

