Abi 2014 Analysis I Teil A: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „__NOTOC__ <div style="padding:1px;background: #EEEEE6;border:0px groove;"> <center><table border="0" width="800px" cellpadding=5 cellspacing=15> <tr><td wid…“) |
|||
| Zeile 22: | Zeile 22: | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
| − | Gegeben ist die Funktion <math>f:x | + | Gegeben ist die Funktion <math>f:x \mapsto \frac{x}{lnx}</math> mit Definitionsmenge IR<sup>+</sup>\{1}. Bestimmen Sie Lage und Art des Extrempunkts des Graphen von f. |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 41: | Zeile 41: | ||
;Aufgabe 2 | ;Aufgabe 2 | ||
| − | Gegeben ist die in IR definierte Funktion f mit | + | Gegeben ist die in IR definierte Funktion f mit <math>f(x) = e^x \cdot (2x + x^2)</math>. |
a) Bestimmen Sie die Nullstellen der Funktion f. | a) Bestimmen Sie die Nullstellen der Funktion f. | ||
| − | b) Zeigen Sie, dass die in IR definierte Funktion F | + | b) Zeigen Sie, dass die in IR definierte Funktion F mit <math>F(x) = x^2 \cdot e^x</math> eine Stammfunktion von f ist. Geben Sie eine Gleichung einer weiteren Stammfunktion G von f an, für die <math>G(1) = 2e</math> gilt. |
| − | + | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 64: | Zeile 63: | ||
;Aufgabe 3 | ;Aufgabe 3 | ||
| − | Gegeben sind die in IR definierten Funktionen | + | Gegeben sind die in IR definierten Funktionen <math>g_a,c : x \mapsto sin(ax) + c</math> mit a,c ∈ IR<sup>+</sup><sub>0</sub>. |
| − | a) Geben Sie für jede der beiden folgenden Eigenschaften einen möglichen Wert für a und einen möglichen Wert für c so an, dass die zugehörige Funktion a, | + | a) Geben Sie für jede der beiden folgenden Eigenschaften einen möglichen Wert für a und einen möglichen Wert für c so an, dass die zugehörige Funktion g<sub>a,c</sub> diese Eigenschaft besitzt. |
| + | <div style="text-indent:20px;">α) Die Funktion g<sub>a,c</sub> hat die Wertemenge [0;2].</div> | ||
| + | <div style="text-indent:20px;">β) Die Funktion g<sub>a,c</sub> hat im Intervall [0;π] genau drei Nullstellen.</div> | ||
| − | b) Ermitteln Sie in Abhängigkeit von a, welche Werte die Ableitung von a, | + | |
| + | b) Ermitteln Sie in Abhängigkeit von a, welche Werte die Ableitung von g<sub>a,c</sub> annehmen kann. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 89: | Zeile 91: | ||
Die Abbildung zeigt den Graphen einer Funktion f. | Die Abbildung zeigt den Graphen einer Funktion f. | ||
| − | a) Beschreiben Sie für | + | a) Beschreiben Sie für a ≤ x ≤ b den Verlauf des Graphen einer Stammfunktion von f. |
b) Skizzieren Sie in der Abbildung den Graphen einer Stammfunktion von f im gesamten dargestellten Bereich. | b) Skizzieren Sie in der Abbildung den Graphen einer Stammfunktion von f im gesamten dargestellten Bereich. | ||
Version vom 7. Juli 2017, 14:01 Uhr
|
|
Gegeben ist die Funktion
|
Gegeben ist die in IR definierte Funktion f mit a) Bestimmen Sie die Nullstellen der Funktion f. b) Zeigen Sie, dass die in IR definierte Funktion F mit |
Gegeben sind die in IR definierten Funktionen a) Geben Sie für jede der beiden folgenden Eigenschaften einen möglichen Wert für a und einen möglichen Wert für c so an, dass die zugehörige Funktion ga,c diese Eigenschaft besitzt. α) Die Funktion ga,c hat die Wertemenge [0;2].
β) Die Funktion ga,c hat im Intervall [0;π] genau drei Nullstellen.
|
"Graph noch einfuegen!" Die Abbildung zeigt den Graphen einer Funktion f. a) Beschreiben Sie für a ≤ x ≤ b den Verlauf des Graphen einer Stammfunktion von f. b) Skizzieren Sie in der Abbildung den Graphen einer Stammfunktion von f im gesamten dargestellten Bereich. |
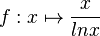 mit Definitionsmenge IR+\{1}. Bestimmen Sie Lage und Art des Extrempunkts des Graphen von f.
mit Definitionsmenge IR+\{1}. Bestimmen Sie Lage und Art des Extrempunkts des Graphen von f.
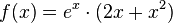 .
.
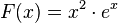 eine Stammfunktion von f ist. Geben Sie eine Gleichung einer weiteren Stammfunktion G von f an, für die
eine Stammfunktion von f ist. Geben Sie eine Gleichung einer weiteren Stammfunktion G von f an, für die 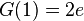 gilt.
gilt.
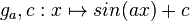 mit a,c ∈ IR+0.
mit a,c ∈ IR+0.

