Abitur Mathematik: Unterschied zwischen den Versionen
| Zeile 31: | Zeile 31: | ||
definierten Funktion <math>w : x \mapsto\sqrt{x}</math> hervorgeht, und geben Sie die | definierten Funktion <math>w : x \mapsto\sqrt{x}</math> hervorgeht, und geben Sie die | ||
Wertemenge von g an. | Wertemenge von g an. | ||
| − | |||
| − | |||
| − | |||
| − | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 70: | Zeile 66: | ||
</td></tr></table></center> | </td></tr></table></center> | ||
| + | </div> | ||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 3 | ||
| + | Geben Sie jeweils den Term einer Funktion an, die über ihrer maximalen | ||
| + | Definitionsmenge die angegebenen Eigenschaften besitzt. | ||
| + | |||
| + | a) Der Graph der Funktion f ist achsensymmetrisch zur y-Achse und die | ||
| + | Gerade mit der Gleichung x 2 ist eine senkrechte Asymptote. | ||
| + | |||
| + | b) Die Funktion g ist nicht konstant und es gilt | ||
| + | |||
| + | g x dx 0. | ||
| + | |||
| + | :{{Lösung versteckt|1= | ||
| + | |||
| + | [[Bild:ABI2017_TeilA_3ab_Lös.jpg|700px]] | ||
| + | |||
| + | }} | ||
| + | |||
| + | </td></tr></table></center> | ||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 4 | ||
| + | |||
| + | |||
| + | :{{Lösung versteckt|1= | ||
| + | |||
| + | [[Bild:ABI2017_TeilA_4ab_Lös.jpg|700px]] | ||
| + | |||
| + | }} | ||
| + | |||
| + | </td></tr></table></center> | ||
</div> | </div> | ||
Version vom 29. Juni 2017, 11:21 Uhr
|
|
Gegeben ist die Funktion a) Geben Sie Dg und die Koordinaten des Schnittpunkts von Gg mit der y-Achse an. b) Beschreiben Sie, wie Gg schrittweise aus dem Graphen der in IR0+
definierten Funktion
|
Eine Funktion f ist durch a) Ermitteln Sie die Nullstelle der Funktion f. b) Die Tangente an den Graphen von f im Punkt S(0 |1) begrenzt mit den beiden Koordinatenachsen ein Dreieck. Weisen Sie nach, dass dieses Dreieck gleichschenklig ist. |
Geben Sie jeweils den Term einer Funktion an, die über ihrer maximalen Definitionsmenge die angegebenen Eigenschaften besitzt. a) Der Graph der Funktion f ist achsensymmetrisch zur y-Achse und die Gerade mit der Gleichung x 2 ist eine senkrechte Asymptote. b) Die Funktion g ist nicht konstant und es gilt g x dx 0. |
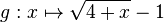 mit maximaler Definitionsmenge
Dg . Der Graph von g wird mit Gg bezeichnet.
mit maximaler Definitionsmenge
Dg . Der Graph von g wird mit Gg bezeichnet.
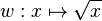 hervorgeht, und geben Sie die
Wertemenge von g an.
hervorgeht, und geben Sie die
Wertemenge von g an.

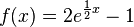 mit x ∈ IR gegeben.
mit x ∈ IR gegeben.




