Abitur Mathematik: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 22: | Zeile 22: | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
| − | Gegeben ist die Funktion <math>g : x \sqrt{4+x} -1</math> mit maximaler Definitionsmenge | + | Gegeben ist die Funktion <math>g : x \mapsto\sqrt{4+x} -1</math> mit maximaler Definitionsmenge |
D<sub>g</sub> . Der Graph von g wird mit G<sub>g</sub> bezeichnet. | D<sub>g</sub> . Der Graph von g wird mit G<sub>g</sub> bezeichnet. | ||
| Zeile 29: | Zeile 29: | ||
b) Beschreiben Sie, wie G<sub>g</sub> schrittweise aus dem Graphen der in IR<sub>0</sub><sup>+</sup> | b) Beschreiben Sie, wie G<sub>g</sub> schrittweise aus dem Graphen der in IR<sub>0</sub><sup>+</sup> | ||
| − | definierten Funktion <math>w : x \sqrt{x}</math> hervorgeht, und geben Sie die | + | definierten Funktion <math>w : x \mapsto\sqrt{x}</math> hervorgeht, und geben Sie die |
Wertemenge von g an. | Wertemenge von g an. | ||
Version vom 29. Juni 2017, 11:12 Uhr
|
|
Gegeben ist die Funktion a) Geben Sie Dg und die Koordinaten des Schnittpunkts von Gg mit der y-Achse an. b) Beschreiben Sie, wie Gg schrittweise aus dem Graphen der in IR0+
definierten Funktion
|
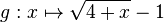 mit maximaler Definitionsmenge
Dg . Der Graph von g wird mit Gg bezeichnet.
mit maximaler Definitionsmenge
Dg . Der Graph von g wird mit Gg bezeichnet.
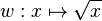 hervorgeht, und geben Sie die
Wertemenge von g an.
hervorgeht, und geben Sie die
Wertemenge von g an.

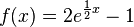 mit x ∈ IR gegeben.
mit x ∈ IR gegeben.


