Q12 Mathematik: Unterschied zwischen den Versionen
(→1. Integralrechnung) |
|||
| Zeile 26: | Zeile 26: | ||
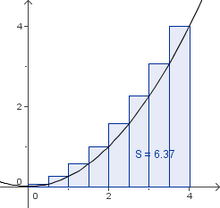
;Unter- und Obersumme | ;Unter- und Obersumme | ||
[[bild:Int_abb1.png|220px|right]] | [[bild:Int_abb1.png|220px|right]] | ||
| − | + | ||
| + | |||
:'''Aufgabe 1''': Gegeben ist die Funktion f(x) = 0.25 x². | :'''Aufgabe 1''': Gegeben ist die Funktion f(x) = 0.25 x². | ||
::#Zerlege das Intervall [0;4] in 8 gleichlange Teilintervalle und skizziere den Graphen und die Rechtecke in dein Heft. | ::#Zerlege das Intervall [0;4] in 8 gleichlange Teilintervalle und skizziere den Graphen und die Rechtecke in dein Heft. | ||
Version vom 18. September 2014, 00:11 Uhr
Hausaufgaben |
1. Integralrechnung
|
2. Binomialverteilung |
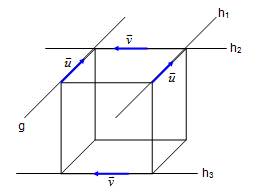
3. Geraden und Ebenen im Raum |
4. Hausaufgaben |
5. Abitur
"Wie schon in der Handreichung anhand von Beispielen erläutert, sind Abituraufgaben vergangener Jahre zur Vorbereitung auf die Abiturprüfung des achtjährigen Gymnasiums geeignet. Grundsätzlich können alle Aufgaben der Grundkurs-Abiturprüfungen der Jahre 2005 bis 2009 zur Vorbereitung genutzt werden. Eine Ausnahme bildet lediglich die Aufgabe 2005 I 3, die mit der zentrischen Streckung einen Inhalt voraussetzt, der nicht Teil des Lehrplans für das achtjährige Gymnasium ist. Die Kombinatorik wird in den künftigen Abituraufgaben ein deutlich geringeres Gewicht haben als bisher; nähere Erläuterungen und Beispielaufgaben dazu finden Sie in der Handreichung. Bei der Auswahl weiterer Aufgaben aus Grundkurs-Abiturprüfungen ist der Lehrplan für das achtjährige Gymnasium zugrunde zu legen. Der Unterschied zwischen Leistungskurs und Grundkurs lag teilweise nur im Umfang der zu behandelnden Inhalte, nicht in deren Schwierigkeitsgrad. Daher können ergänzend einzelne, mit dem Lehrplan für das achtjährige Gymnasium vereinbare Aufgaben aus Leistungskurs-Abiturprüfungen zur Vorbereitung herangezogen werden, ohne dass das Niveau des bisherigen Grundkurses zwangsläufig überschritten wird. Geeignet sind
|
- Kapitel aus dem Buch: Kapitel 2
 0,5 + f (1)
0,5 + f (1)