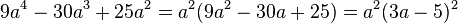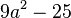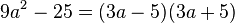Term und Zahl: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(→‎Teste dein Wissen)
Zeile 68: Zeile 68:
 
<math>9a^4-30a^3+25a^2 </math>
 
<math>9a^4-30a^3+25a^2 </math>
 
<popup name = "Lösung">
 
<popup name = "Lösung">
 +
<math> 9a^4-30a^3+25a^2=(3a^2-5a)^2  </math> 2. binomische Formel <br/>
 
<math> 9a^4-30a^3+25a^2=a^2(9a^2-30a+25)=a^2(3a-5)^2 </math> <br/> a<sup>2</sup> ausklammern +2.binomische Formel
 
<math> 9a^4-30a^3+25a^2=a^2(9a^2-30a+25)=a^2(3a-5)^2 </math> <br/> a<sup>2</sup> ausklammern +2.binomische Formel
 
</popup><br/>
 
</popup><br/>

Version vom 11. September 2014, 19:41 Uhr


Teste dein Wissen


1.Vereinfache folgende Terme soweit wie möglich.
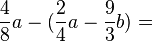
\frac48 a-( \frac24 a- \frac93 b) =


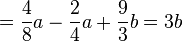
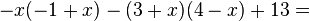
-x(-1+x)-(3+x)(4-x)+13=


2.Setze im ersten Term die Klammern so, dass eine richtige Termumformung entsteht.
-2a^2+4a \cdot 2 - a = 8a


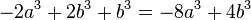
-2a^3+2b^3+b^3 = -8a^3+4b^3


3.Klammere den größtmöglichen Faktor aus.
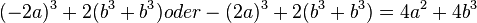
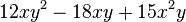
 12xy^2-18xy+15x^2y


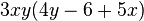
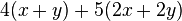
4(x+y)+5(2x+2y)


Knicktests





Knicktest Termumformungen, Faktorisieren



4.Faktorisiere den Term (mit Hilfe der binomischen Formeln).
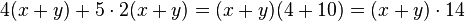
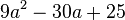
 9a^2-30a+25


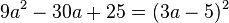
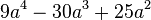
9a^4-30a^3+25a^2


9a^2-25


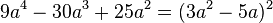Knicktest Binomische Formeln



5. Gib die Definitionsmenge an und vereinfache soweit wie möglich.
 \frac{32a^2+a}{a}


\frac{x^4}{x^6(x-2)}


Knicktest Bruchterme



6) Vereinfache soweit wie möglich (a>0)
\sqrt a \cdot (\sqrt a)^3 a^{-3}


(16^{\frac1 4} a^{\frac1 a})^4


8^x:2^x


Knicktest Potenzen und Wurzeln

Zurück zur Übersicht

Von „http://rmg.zum.de/index.php?title=Mathematik_Grundwissen_10/Term_und_Zahl&oldid=58460“