Archimedische Körper: Unterschied zwischen den Versionen
(→Kuboktaeder) |
(→Kuboktaeder) |
||
| Zeile 118: | Zeile 118: | ||
{| class="" style="text-align:center" style="background:#F0E9CA" | {| class="" style="text-align:center" style="background:#F0E9CA" | ||
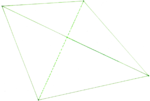
| − | |style="background:#F0E9CA"| [[File:Uniform polyhedron-43-t0.svg|x50px]] + [[File:Uniform polyhedron-43-t2.svg|x50px]] «» [[ | + | |style="background:#F0E9CA"| [[File:Uniform polyhedron-43-t0.svg|x50px]] + [[File:Uniform polyhedron-43-t2.svg|x50px]] «» [[Datei:Kuboktaeder.png|x50px]] |
<font size = "1">Abb.: 13.13 Tetraeder «» Tetraederstumpf </font> | <font size = "1">Abb.: 13.13 Tetraeder «» Tetraederstumpf </font> | ||
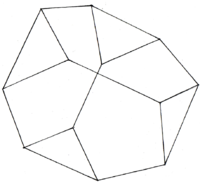
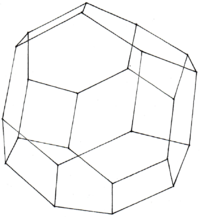
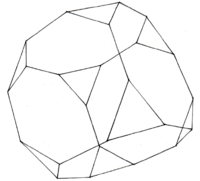
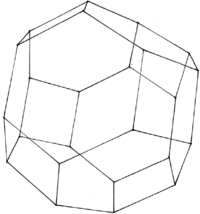
| rowspan="2" style="background:#F0E9CA" | Der Kuboktaeder besitzt als Ausgangskörper den Tetraeder oder Hexaeder und Oktaeder (,welche sich beide Durchdringen). | | rowspan="2" style="background:#F0E9CA" | Der Kuboktaeder besitzt als Ausgangskörper den Tetraeder oder Hexaeder und Oktaeder (,welche sich beide Durchdringen). | ||
Version vom 12. November 2013, 07:43 Uhr
|
|
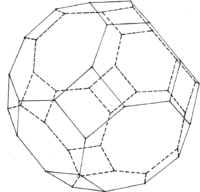
TetraederstumpfKuboktaeder
Hexaederstumpf
Oktaederstumpf
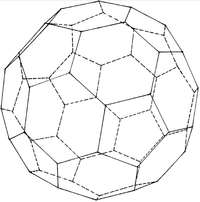
(Kleines) RhombenkuboktaederGroßes Rhombenkuboktaeder
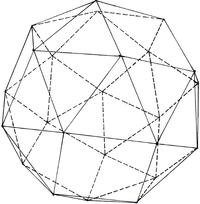
IkosidodekaederDodekaederstumpfIkosaederstumpf
Abgeschrägtes Hexaeder
(Kleines) Rhombenikosidodekaeder
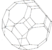
Großes RhombenikosidodekaederAbgeschrägtes DodekaederFile:Trunc-icosa.jpg
|